Прочтите прежде чем задавать вопрос!
Прочтите прежде чем задавать вопрос!
1. Заголовок темы должен быть информативным. В противном случае тема удаляется ...
2. Все тексты программ должны помещаться в теги [code=pas] ... [/code].
3. Прежде чем задавать вопрос, см. "FAQ", если там не нашли ответа, воспользуйтесь ПОИСКОМ, возможно такую задачу уже решали!
4. Не предлагайте свои решения на других языках, кроме Паскаля (исключение - только с согласия модератора).
5. НЕ используйте форум для личного общения, все что не относится к обсуждению темы - на PM!
6. Одна тема - один вопрос (задача)
7. Проверяйте программы перед тем, как разместить их на форуме!!!
8. Спрашивайте и отвечайте четко и по существу!!!
  |
| Altair |
 27.11.2005 23:54 27.11.2005 23:54
Сообщение
#1
|
 Ищущий истину       Группа: Модераторы Сообщений: 4 824 Пол: Мужской Реальное имя: Олег Репутация:  45 45  |
задача
Дано множество точек в простанстве. Определить координаты n-угольника максимальной площади с вершинами в данных точках. Если бы задача решалась на плоскости, то все тривиально - строим выпуклую оболочку и вот нам многоугольник макс. площади. Программа:  p.pas ( 4.72 килобайт )
Кол-во скачиваний: 602
p.pas ( 4.72 килобайт )
Кол-во скачиваний: 602Сриншеты:  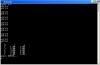 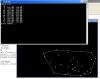 EXE и исходники в архиве:  p.zip ( 33.28 килобайт )
Кол-во скачиваний: 385
p.zip ( 33.28 килобайт )
Кол-во скачиваний: 385Вопрос вот в чем... какой же алгоритм стоит применить когда речь о пространстве ? Одна из сложностей - площадь мы все равно можем считать только плоской фигуры, а сколько плоскостей надо перебрать в пространстве только для того что бы на каждой искать выпуклую облочку.. ясно что задача решается как то по другому... в какую сторону копать ? p.s. спасибо одной девушке за любезно предоставленную задачу То , что многоугольник обязан быть выпуклым доказывается очень просто. Предположим что макс. площадь достигаается невыпуклым: 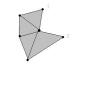 но тогда соединив точки 1 2 мы получим выпуклый, причем с большей плозадью. -------------------- Помогая друг другу, мы справимся с любыми трудностями!
"Не опускать крылья!" (С) |
| Altair |
 28.01.2006 20:47 28.01.2006 20:47
Сообщение
#2
|
 Ищущий истину       Группа: Модераторы Сообщений: 4 824 Пол: Мужской Реальное имя: Олег Репутация:  45 45  |
Как вариант решения задачи, было предложенно (mo3r)
перебирать тройки точек, и для каждой тройки определить, какие вершины лежат с ними в одной плоскости, и построить их выпуклую оболочку. Временная сложность: O(n^4*log(n)) (n^3 троек, на каджую тройку - n*log(n)). -------------------- Помогая друг другу, мы справимся с любыми трудностями!
"Не опускать крылья!" (С) |
| hardcase |
 29.01.2006 12:13 29.01.2006 12:13
Сообщение
#3
|
 code warrior     Группа: Пользователи Сообщений: 484 Пол: Мужской Реальное имя: Славен Репутация:  8 8  |
А если не перебирать все точки сразу, а построить выпуклую оболочку для всего множества, и потом к ней применить приведённый выше алгоритм?
Или можно строить не оболочку, а выбирать точки по определённому критерию - отметать все заведомо лежащие внутри фигуры точки. Сообщение отредактировано: hardcase - 29.01.2006 12:15 -------------------- ИзВ ин ИтЕ зА нЕ рОв НЫй П оч ЕРк
|
| Altair |
 29.01.2006 13:09 29.01.2006 13:09
Сообщение
#4
|
 Ищущий истину       Группа: Модераторы Сообщений: 4 824 Пол: Мужской Реальное имя: Олег Репутация:  45 45  |
hardcase, ты абсолютно прав, но
1. алгоритма построения выпуклой оболочки в пространстве нет. 2. если ты построишь его, то не факт , что по скорости весь алгоритм будет быстее.. -------------------- Помогая друг другу, мы справимся с любыми трудностями!
"Не опускать крылья!" (С) |
  |
1 чел. читают эту тему (гостей: 1, скрытых пользователей: 0)
Пользователей: 0

|
Текстовая версия | 14.08.2025 5:49 |