  |
| Ars |
 19.06.2005 17:04 19.06.2005 17:04
Сообщение
#1
|
|
Группа: Пользователи Сообщений: 7 Пол: Мужской Репутация:  0 0  |
Кто может сказать как решаются задачи:
1) О Кенигсбергских мостах. Обойти все четыре части суши, пройдя по каждому мосту один раз, и вернуться в исходную точку. 2) Задача о трех домах и трех колодцах. Имеется три дома и три колодца. Провести от каждого дома к каждому колодцу тропинку так, чтобы тропинки не пересекались. Эскизы прикрепленных изображений 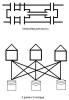
|
| volvo |
 19.06.2005 17:16 19.06.2005 17:16
Сообщение
#2
|
|
Гость |
С домами - вот так:
Эскизы прикрепленных изображений 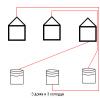
|
| virt |
 19.06.2005 19:28 19.06.2005 19:28
Сообщение
#3
|
 Знаток     Группа: Пользователи Сообщений: 419 Пол: Мужской Репутация:  6 6  |
volvo
Цитата от каждого дома к каждому колодцу Граф в задаче о домах по другому называется граф K(3,3) и не может быть представлен в виде планарного. -------------------- |
| Altair |
 19.06.2005 20:56 19.06.2005 20:56
Сообщение
#4
|
 Ищущий истину       Группа: Модераторы Сообщений: 4 824 Пол: Мужской Реальное имя: Олег Репутация:  45 45  |
Цитата О Кенигсбергских мостах это эйлеров цикл... -------------------- Помогая друг другу, мы справимся с любыми трудностями!
"Не опускать крылья!" (С) |
| Ars |
 20.06.2005 20:40 20.06.2005 20:40
Сообщение
#5
|
|
Группа: Пользователи Сообщений: 7 Пол: Мужской Репутация:  0 0  |
Цитата это эйлеров цикл... А в чем он заключается? |
| Ars |
 20.06.2005 20:43 20.06.2005 20:43
Сообщение
#6
|
|
Группа: Пользователи Сообщений: 7 Пол: Мужской Репутация:  0 0  |
volvo
Честно говоря, я не понял решения... |
| Altair |
 20.06.2005 21:37 20.06.2005 21:37
Сообщение
#7
|
 Ищущий истину       Группа: Модераторы Сообщений: 4 824 Пол: Мужской Реальное имя: Олег Репутация:  45 45  |
Цитата §1. Основные понятия и определения Дадим теперь строгое определение эйлерову циклу и эйлерову графу. Если граф имеет цикл (не обязательно простой), содержащий все ребра графа по одному разу, то такой цикл называется эйлеровым циклом, а граф называется эйлеровым графом. Если граф имеет цепь (не обязательно простую), содержащую все вершины по одному разу, то такая цепь называется эйлеровой цепью, а граф называется полуэйлеровым графом. Ясно, что эйлеров цикл содержит не только все ребра по одному разу, но и все вершины графа (возможно, по несколько раз). Очевидно также, что эйлеровым может быть только связный граф. Выберем в качестве вершин графа берега реки, а в качестве ребер - мосты, их соединяющие. После этого задача становится очевидной: требование неосуществимо - чтобы его выполнить, число дуг, приходящих к каждой вершине, должно быть четным. В самом деле, поскольку по одному мосту нельзя проходить дважды, каждому входу на берег должен соответствовать выход. §2. Критерий существования эйлерова цикла Что необходимо, чтобы в графе существовал эйлеров цикл? Во-первых, граф должен быть связанным: для любых двух вершин должен существовать путь, их соединяющий. Во-вторых, для неориентированных графов число ребер в каждой вершине должно быть четным. На самом деле этого оказывается достаточно. Теорема 1. Чтобы в связанном неориентированном графе G существовал эйлеров цикл, необходимо и достаточно, чтобы число вершин нечетной степени было четным. Доказательство. Необходимость. Любой эйлеров цикл должен прийти в вершину по одному ребру и покинуть ее по другому, так как любое ребро должно использоваться ровно один раз. Поэтому, если G содержит эйлеров цикл, то степени вершин должны быть четными. Достаточность. Пусть G — связный неориентированный граф, все вершины которого имеют четную степень. Начнем путь из некоторой произвольной вершины x0 и пойдем по некоторому ранее не использованному ребру к следующей вершине, и так до тех пор, пока не вернемся в вершину x0 и не замкнем цикл. Если все ребра окажутся использованными, то нужный эйлеров цикл построен. Если же некоторые ребра не использованы, то пусть Ф — только что построенный цикл. Так как граф G связен, то цикл Ф должен проходить через некоторую вершину, скажем xi, являющуюся конечной вершиной какого-либо до сих пор не использованного ребра. Если удалить все ребра, принадлежащие Ф, то в оставшемся графе все вершины по-прежнему будут иметь четную степень, так как в цикле Ф должно быть четное число ребер (0 является четным числом), инцидентных каждой вершине. Начиная теперь с xi, получаем цикл Ф’, начинающийся и оканчивающийся в xi. Если все оставшиеся ранее ребра использованы для цикла Ф’, то процесс окончен. Нужный эйлеров цикл будет образован частью цикла Ф от вершины x0 до xi, затем циклом Ф’ и, наконец, частью цикла Ф от вершины xi до x0. Если же все еще остались неиспользованные ребра, то объединение построенных выше циклов Ф и Ф’ дает новый цикл Ф. Мы снова можем найти вершину xj, принадлежащую циклу и являющуюся концевой вершиной некоторого неиспользованного ребра. Затем мы можем приступить к построению нового цикла Ф’, начинавшегося в xj, и так до тех пор, пока не будут использованы все ребра и не будет получен таким образом эйлеров цикл Ф. Это доказывает теорему. Хотя доказательство проведено для неориентированных графов, оно сразу переносится на ориентированные, только требование четности заменяется теперь на такое: число входящих в каждую вершину ребер должно быть равно числу выходящих. Следствие #1. Для связного эйлерова графа G множество ребер можно разбить на простые циклы. Следствие #2. Для того чтобы связный граф G покрывался единственной эйлеровой цепью, необходимо и достаточно, чтобы он содержал ровно 2 вершины с нечетной степенью. Тогда цепь начинается в одной из этих вершин и заканчивается в другой. §3. Алгоритмы построения эйлерова цикла Выше был установлен эффективный способ проверки наличия эйлерова цикла в графе. А именно, для этого необходимо и достаточно убедиться, что степени всех вершин четные, что нетрудно сделать при любом представлении графа. Осталось заметить, что предложенный в доказательстве алгоритм линеен, т.е. число действий прямо пропорционально числу ребер. Алгоритм построения эйлерова цикла в эйлеровом графе. Вход: эйлеров граф G(V,E), заданный матрицей смежности. Для простоты укажем, что Г[v]— множество вершин, смежных с вершиной v. Выход: последовательность вершин эйлерова цикла. S:=Ø {стек для хранения вершин} select v V {произвольная вершина} v→S {положить v в стек S} while S≠Ø do v←S; v→S {v — верхний элемент стека} if Г[v]=Ø then v←S; yield v else select u Г[v] {взять первую вершину из списка смежности} u→S {положить u в стек} Г[v]:=Г[v]\{u}; Г[u]:=Г[u]\{v} {удалить ребро (v,u)} end if end while + http://forum.pascalnet.ru/index.php?showt...indpost&p=42495 -------------------- Помогая друг другу, мы справимся с любыми трудностями!
"Не опускать крылья!" (С) |
  |
1 чел. читают эту тему (гостей: 1, скрытых пользователей: 0)
Пользователей: 0

|
Текстовая версия | 9.07.2025 18:47 |








