 Прочтите прежде чем задавать вопрос!
Прочтите прежде чем задавать вопрос!
1. Заголовок темы должен быть информативным. В противном случае тема удаляется ...
2. Все тексты программ должны помещаться в теги [code=pas] ... [/code].
3. Прежде чем задавать вопрос, см. "FAQ", если там не нашли ответа, воспользуйтесь ПОИСКОМ, возможно такую задачу уже решали!
4. Не предлагайте свои решения на других языках, кроме Паскаля (исключение - только с согласия модератора).
5. НЕ используйте форум для личного общения, все что не относится к обсуждению темы - на PM!
6. Одна тема - один вопрос (задача)
7. Проверяйте программы перед тем, как разместить их на форуме!!!
8. Спрашивайте и отвечайте четко и по существу!!!
  |
| Michael_Rybak |
 16.11.2006 23:25 16.11.2006 23:25
Сообщение
#21
|
|
Michael_Rybak      Группа: Модераторы Сообщений: 1 046 Пол: Мужской Реальное имя: Michael_Rybak Репутация:  32 32  |
Там *не все* связано с разибиением на поддеревья. Просто проиндескируй оба дерева, и посмотри, равны ли индексы. Если ты потратишь хоть немного времени и разберешься в том, что я написал, ты поймешь, что это именно то, что тебе нужно.
|
| Маня |
 18.11.2006 19:30 18.11.2006 19:30
Сообщение
#22
|
|
Группа: Пользователи Сообщений: 9 Пол: Женский Репутация:  1 1  |
понимаешь,я уже несколько раз все твои сообщения прочитала,но толком ничего не поняла...
Во-первых как по матрице смежности мы будем находить корневую или концевые вершины? Во-вторых, а если корневых вершин две? Я поняла,что надо взять концевые вершины,проиндексировать их через (0) Потом как мы достаиваем ребро? -------------------- Потому что, потому что
Всех нужнее и дороже, Всех доверчивей и строже В этом мире доброта В этом мире ДОБРОТА |
| Michael_Rybak |
 19.11.2006 2:01 19.11.2006 2:01
Сообщение
#23
|
|
Michael_Rybak      Группа: Модераторы Сообщений: 1 046 Пол: Мужской Реальное имя: Michael_Rybak Репутация:  32 32  |
Давай разберемся с тем, что я называю индексацией. Индексация - это присвоение индексов (номеров) поддеревьям так, чтобы изоморфным поддеревьям соответствовали одинаковые индексы, а не изоморфным - разные.
В случае графа "без корня" это делается путем сворачивания листьев в каждом из двух графов. Смотри. Пусть у нас есть графы А и В. На первом шагу ничего еще не свернули. Считаем, сколько листьев в А и в В. Если количества листьев - разные, то уже понятно, что графы неизоморфны. Иначе говорим, что все листы получают индекс 0. Теперь сворачиваем все листы. Сворачиваем - это значит "приклеиваем" индекс листа к той вершине, к которой ведет единственное ребро из этого листа, а сам лист удаляем вместе с этим ребром. Например, если какая-то вершина была соединена с двумя листьями и тремя не-листьями, то те два листа (с их индексами 0) мы приклеим к ней, а три других ребра останутся. Теперь в каждом графе появились новые листья (благодаря сворачиванию листьев на предыдущем шаге). Листьев опять должно быть поровну (если нет - сразу не изоморфны). Но теперь этого уже не достаточно. Кроме того, что листьев должно быть поровну, листья должны быть еще и попарно равными. А именно: к некоторым листьям "приклеился" один лист на прошлом этапе, к некоторым - больше. Такие "свертыши" нужно отличать друг от друга. Вот здесь и начинается индексация. Берем любой лист-"свертыш". Смотрим, что к нему там приклеено, т.е. записываем индексы приклееных к нему листьев, например (0; 0; 0). Сортируем их (индексы) по возрастанию, и даем ему индекс 1. Теперь, если мы встретим когда-либо еще один лист-свертыш, к которому было приклеено (0; 0; 0), это будет означать, что он изоморфен этому, и ему мы тоже дадим индекс 1. Прочитав досюда, теперь попробуй еще раз прочесть мой самый первый пост. Там я на примере сравниваю два дерева с корнями, хотя наличие корней, по большому счету, не использую (просто идем вглубь, сворачивая). Чтобы узнать, изоморфны ли сравниваемые деревья, нужно просто посмотреть, равны ли их индексы. |
| Маня |
 19.11.2006 23:48 19.11.2006 23:48
Сообщение
#24
|
|
Группа: Пользователи Сообщений: 9 Пол: Женский Репутация:  1 1  |
Ой !!! Спасибо огромное!
Знаешь,а у меня задание изоморфизм ОРИЕНТИРОВАННЫХ деревьев. Пример, есть такое дерево:оно в добавленных файлах. Проиндексируем все листики,значит 1(0),4(0),8(0).Будем смотреть как связаны вершины. Если ребро идёт из листа к корню,то 1,если наоборот,то 2 ,если в обе стороны,то 3. Получаем - 2(0,1), 3(0,3), 7 (0,3). Теперь (0,1)-4,(0,2)-5, (0,3)-6. Получаем - 2(4),3(6),7(6). Дальше (1,4)-7,(1,5)-8,(1,6)-9,(2,4)-10,...,(3,6)-15...Чё-то слишком много получается, а чем дальше, тем хуже...5(12,13)....что-то сложновато получается....ЧТО делать? Эскизы прикрепленных изображений 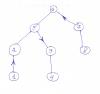
-------------------- Потому что, потому что
Всех нужнее и дороже, Всех доверчивей и строже В этом мире доброта В этом мире ДОБРОТА |
| Michael_Rybak |
 20.11.2006 2:17 20.11.2006 2:17
Сообщение
#25
|
|
Michael_Rybak      Группа: Модераторы Сообщений: 1 046 Пол: Мужской Реальное имя: Michael_Rybak Репутация:  32 32  |
Молодец, Маня, порадовала!
Цитата Если ребро идёт из листа к корню,то 1,если наоборот,то 2 ,если в обе стороны,то 3. Да, очень правильная мысль. Цитата Чё-то слишком много получается, а чем дальше, тем хуже... Согласен. А знаешь, почему? Потому что в том-то вся прелесть, что индексировать надо только то, что встретилось, а не все возможные комбинации. Например, ты говоришь: (0,1)-4,(0,2)-5, (0,3)-6. А зачем тебе (0,2)-5, если такого в графе нету? Поправляем твои рассуждения с этой точки зрения. Проиндексируем все листики, значит 1(0),4(0),8(0). Будем смотреть как связаны вершины. Если ребро идёт из листа к корню,то 1,если наоборот,то 2 ,если в обе стороны,то 3. Сворачиваем. Листьями становятся вершины 2, 3 и 7. У двойки приклеено (0,1). Даем вершине, к которой приклеено (0,1), следующий неиспользованный индекс, т.е. 1. У тройки приклеено (0,3). Даем вершине, к которой приклеено (0,3), следующий неиспользованный индекс, т.е. 2. У семерки приклеено (0,3). Даем вершине, к которой приклеено (0,3), следующий неиспользованный индекс, СТОП! Это мы уже делали - вершина, к которой приклеено (0,3) уже имеет индекс 2. Получаем - 2(1), 3(2), 7(2). На следующем этапе листьями становятся 5 и 6. К пятерке приклеено (1,3) и (2,2). Вершине, к которой приклеено (1,3) и (2,2), дадим следующий неиспользованный индекс, т.е. 3. К шестерке приклеено (2,1). Вершине, к которой приклеено (2,1), дадим индекс 4. Получаем - 5(3), 6(4). Процесс свертки заканчивается, когда всё свернется либо в одну точку, либо в две (как в нашем случае). Теперь всему графу ставим в соответствие новый индекс: "Графу, свернувшемуся в пару 3 и 4 (помним, что это - индексы пятерки и шестерки соответственно), соединенную ребром вида 3, ставим в соответствие следующий неиспользованный индекс, т.е. 5". Вышла такая табличка: 0 - лист 1 - (0,1) 2 - (0,3) 3 - (1,3) и (2,2) 4 - (2,1) 5 - граф, свернувшийся в пару 3-4, соединенную ребром вида 3 Теперь делаем то же самое с другим графом, причем табличку строим не заново, а продолжаем строить эту! Если они изоморфны, то в конце он тоже свернется в пару 3-4, соединенную ребром вида 3, и получит индекс 5. Еще важная деталь: если у нас встретится вершина, к которой приклеено (1,3) и (2,2), мы ей дадим индекс 3, т.к. это уже было. Но если у нас встретится вершина, к которой приклеено (2,2) и (1,3), мы должны ей тоже дать индекс 3, потому что это - то же самое. Именно поэтому перед тем, как смотреть, что там у нас приклеено, надо отсортировать список приклееных пар (по возрастанию номера, например), т.е. установить канонический порядок их следования. |
| Маня |
 22.11.2006 22:26 22.11.2006 22:26
Сообщение
#26
|
|
Группа: Пользователи Сообщений: 9 Пол: Женский Репутация:  1 1  |
Просто СУПЕР!!! ВСЁ поняла! но,естественно, возникли другие проблемы....как ты,например,посоветуешь ввести данные,т.е. через матрицу смежности или FO-представление? Ещё вопросик: когда мы индексируем,это значит,что мы записываем в массив эти данные или же какой-нибудь список сделать? Жду твоих советов и помощи! -------------------- Потому что, потому что
Всех нужнее и дороже, Всех доверчивей и строже В этом мире доброта В этом мире ДОБРОТА |
| Маня |
 22.11.2006 23:26 22.11.2006 23:26
Сообщение
#27
|
|
Группа: Пользователи Сообщений: 9 Пол: Женский Репутация:  1 1  |
О!!! У меня родилась идея,точнее мысль
Примеры графов в прикрепленных файлах. Выходит,что у первого графа итог 5- (3,4), соедин. 3, у второго 5-(3,4), соедин. 3,выходит,что они изоморфны, но даже по рисункам с первого взгляда видно, что они неизоморфны.Что это значит? Что способ неверен? или же мы проверяем не только конечный итог, но весь массив? Для первого это: 0-лист 1-(0,1) 2-(0,3) 3-(1,3) (2,2) 4-(2,1) 5-(3,4) Для второго: 0-лист 1-(0,1) 2-(0,3) 3-(1,3) 4-(2,2) 5-(3,4) 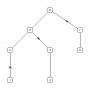 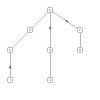 -------------------- Потому что, потому что
Всех нужнее и дороже, Всех доверчивей и строже В этом мире доброта В этом мире ДОБРОТА |
| Michael_Rybak |
 23.11.2006 4:33 23.11.2006 4:33
Сообщение
#28
|
|
Michael_Rybak      Группа: Модераторы Сообщений: 1 046 Пол: Мужской Реальное имя: Michael_Rybak Репутация:  32 32  |
Молодец что придумала пример
Цитата Теперь делаем то же самое с другим графом, причем табличку строим не заново, а продолжаем строить эту! Если они изоморфны, то в конце он тоже свернется в пару 3-4, соединенную ребром вида 3, и получит индекс 5. Видишь? Не заново, а продолжаем строить эту! Что касается реализации - на паскале я бы сначала слегка застрелился, а потом бы уже писал. STL все-таки страшно развращает. Ты на чем собралась писать? Граф я храню FO представлением, но таким двойным: из каждой вершины помню все ребра, и входящие, и исходящие. Каждое ребро, таким образом, встречается 2 раза. При этом на каждом ребре ставлю отметку, какое оно (туда, обратно или в обе стороны). Результат свертки для каждой вершины храню отдельной структурой (динамическим массивом, содержащим в порядке возрастания индексы приклееных вершин). |
| Маня |
 28.11.2006 11:26 28.11.2006 11:26
Сообщение
#29
|
|
Группа: Пользователи Сообщений: 9 Пол: Женский Репутация:  1 1  |
Значится так, вот как я поняла этот алгоритм:
1. сравниваем кол-во вершин в обоих графах,если разное, то неизоморфны,иначе 2. находим концевые вершины 3. сравниваем кол-во концевых вершин в обоих графах, если разное, то неизоморфны,иначе 4. индексируем их,т.е. записываем в динамический массив данные о вершине, например vershina^[1].Name:='1'; vershina^[1].indeks:=0 5. смотрим,с какими вершинами соединены концевые вершины и рёберную связь между ними (если выходит - 1, входит - 2, двусторон. - 3) 6. запишем эту информацию просто в массив,который будет хранить значения индексов,значит у нас (0,1) - 1 7. сравниваем кол-во вершин,соедин. с концевыми вершинами в обоих графах,если разное, то неизоморфны,иначе 8. записываем эту информацию к вершинам vershina^[2].Name:='2'; vershina^[2].indeks:=1; В ИТОГЕ МЫ ПОЛУЧАЕМ ПРОЦЕДУРУ,СОСТОЯЩУЮ ИЗ 3-Х ПУНКТОВ,КОТОРУЮ НУЖНО ПРОКРУЧИВАТЬ В ЦИКЛЕ. 9. у нас получатся 2 динамических массива 10. начинаем сравнивать эти 2 массива,как сравнивать я призабыла...к вечеру разберусь Так вот... Ну как? Правильно ли я поняла? Вот вопросик: -------------------- Потому что, потому что
Всех нужнее и дороже, Всех доверчивей и строже В этом мире доброта В этом мире ДОБРОТА |
| Michael_Rybak |
 28.11.2006 14:46 28.11.2006 14:46
Сообщение
#30
|
|
Michael_Rybak      Группа: Модераторы Сообщений: 1 046 Пол: Мужской Реальное имя: Michael_Rybak Репутация:  32 32  |
Схему ты описала правильно, но вот правильно ли ты понимаешь центральное место - индексацию вершины - я не очень понял.
Мне кажется, тут нужен один большой динамический массив, каждый элемент которого - это набор пар (индекс-ребро), свернувшихся в некоторую вершину. Вот в нашей табличке: 0-лист 1-(0,1) 2-(0,3) 3-(1,3) (2,2) 4-(2,1) 5-(3,4) Каждая строка здесь - это элемент вот этого динамического массива. Типа такого: type TPair = record //структура для хранения одного "свернутого" объекта На каждой итерации ты все глубже залазишь в граф, сворачивая листы, появившиеся после предыдущей итерации. У каждой вершины на протяжении этого процесса хранится ее TBlock, в котором index пока что неивестен, а kids заполняется. Когда ты сворачиваешь лист, ты смотришь, к какой вершине он свернется, и вписываешь этот лист к блоку той вершины, в которую он свернется (вместе с типом ребра). Т.е. ты еще в начале объявляешь массив блоков: var b: array [1..n] of TBlock; В начале все блоки пусты. Когда вершина i сворачивается к вершине j, то в блок b[j] дописывается в поле kids пара TPair, в которой child_index - это индекс, присвоенный вершине i, а type_of_edge - тип ребра, соединяющего i и j. А когда j станет листом (т.е. все связанные с ней вершины, кроме одной, свернутся в нее), то в b[j].index мы запишем его индекс, полученный путем поиска b[j] в массиве a, т.е. в нашей табличке. Короче, Маня. Знаешь, с чего начни. Начни с того, что напиши программу, которая просто сворачивает граф. Т.е. на входе - ФО представление, на выходе что-то такое: Код Шаг 1 Листы: 1 2 5 9 В лист 1 свернулись: В лист 2 свернулись: В лист 5 свернулись: В лист 9 свернулись: Шаг 2 Листы: 3 4 7 В лист 3 свернулись: 1 2 В лист 4 свернулись: 9 В лист 7 свернулись: 5 Шаг 3 Листы 6 8 В лист 6 свернулись: 3 7 В лист 8 свернулись: 4 Итог: Граф свернулся в ребро, соединяющее вершины 6 и 8. Т.е. никакой индексации, просто свертка. Цитата как по FO-представлению мы можем найти концевые вершинки? Можно так. Заведи массив start[n], в котором в start[i] хранится начало списка достижимых из i вершин (в FO представлении). Например FO представление: 5 2 3 0 5 0 1 0 3 0 0 start[1] = 1 start[2] = 4 start[3] = 6 start[4] = 8 start[5] = 10 Теперь чтобы узнать, какие ребра идут из вершины x, мы идем по ФО прелставлению, начиная с позиции start[x], и пока не встретим 0. Чтобы узнать, какая вершина является листиком, надо посчитать, сколько несвернутых вершин с ней соединены. |
  |
1 чел. читают эту тему (гостей: 1, скрытых пользователей: 0)
Пользователей: 0

|
Текстовая версия | 14.08.2025 2:21 |








