диф.уры, геометрчиеская задача Опции

[3 kilos]

Записать уравнение кривой, если известно. что точка пересечения любой касательной к кривой с осью абцисс одинаково удалена от точки касания и от начала координат.

Можете подсказать как подходить к задаче? А то ничего на ум не приходит вообще.

задача на составления диф. уравнения =)

Сообщение отредактировано: 3 kilos - 23.04.2006 19:10

[Lapp]

Все становится довольно прозрачным, стоит лишь сделать рисунок.

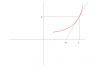Кривая (красная) взята от балды, с реальным ответом она вряд ли имеет много общего. А вот касательная к ней очень даже существенна. Она пересекает абсциссу в х=а. Далее, мы знаем, что производная равна тангенсу угла наклона касательной:

y' = y/(x-a)

Это и есть искомое уравнение, но в нем пока присутствует инородный элемент, a. Надо выразить его через x и y. Делаем это из условия, что точка a равноудалена от точки графика и начала координат.

a^2 = (x-a)^2

Раскрываем скобку:

a^2 = x^2 - 2xa + a^2 + y^2

Квадраты а^2 уничтожаются, после чего a легко выражается:

a = (x^2 + y^2)/(2x)

Подставив это в выражение для y', получим ответ.
Для исследования полноты картины рекомендую нарисовать аналогичную картинку во всех четырех квадрантах.

[3 kilos]

lapp

Спасибо огромное, диф ур уж я решу =)

А у меня однако мысли немного подругому пошли, странно получилось, диф.ур я тоже получил, но чет не верится что эти диф-уры тождественны.

Сообщение отредактировано: 3 kilos - 25.04.2006 7:52