  |
| virt |
 12.02.2005 17:57 12.02.2005 17:57
Сообщение
#1
|
 Знаток     Группа: Пользователи Сообщений: 419 Пол: Мужской Репутация:  6 6  |
Графы можно представлять в виде множества вершин и множества соединяющих их ребер. (Города и дороги их соединяющие)
1. Просмотр вершин графа в некотором фиксированном порядке. общие структуры данных : const Maxn=100; поиск в глубину :
Поиск в ширину: procedure Pw(v:integer); 2. Каркасы (стягивающие деревья) const Maxn=100; Построение стягивающего дерева поиском в глубину: procedure Tree_Depth(v:integer); Построение стягивающего дерева поиском в ширину: procedure Tree_Width(v:integer); Построение всех каркасов графа: const Maxn=100; Построение минимального каркаса методом Краскала: (Исправлено. Присоединенный архив перезалит) Граф задан списком ребер с указанием их весов: program minim_tree_kraskal; Построение минимального каркаса методом Прима: procedure solve; Сообщение отредактировано: volvo - 13.01.2009 11:36 Прикрепленные файлы  graph.zip ( 2.67 килобайт )
Кол-во скачиваний: 1520
graph.zip ( 2.67 килобайт )
Кол-во скачиваний: 1520-------------------- |
| Altair |
 5.05.2005 15:02 5.05.2005 15:02
Сообщение
#2
|
 Ищущий истину       Группа: Модераторы Сообщений: 4 824 Пол: Мужской Реальное имя: Олег Репутация:  45 45  |
Поиск кратчайших путей.
Алгоритм Флойда Описание алгоритма: Над матрицей A (NxN) выполняется n итераций. После k-ой итерации, A[i,j] содержит значение наименьшей длинны путей из вершины i в вершину j, которые не проходят через вершины с номером, большим k. На k-ой итерации для вычисления матрицы A, используется слудующая формула: Ak[i,j] = min (Ak-1[i,j], Ak-1[i,k]+ Ak-1[k,j]). Графическая интерпретация формулы: Сложность алгоритма Время выполнения программы, имеетпорядок O(n3), так как в ней нет практически ничего, кроче 3 вложенных друг в друга циклов. Сохранение маршрутов. Что бы сохранять маршруты, от одной вершины кдругой, следует, ввести еще одну матрицу, в которой каждому элементу P[I,j]присваивать вершину K (номер), полученную при нахождении наименьшего значения a[I,j]. Const В программе C-граф, заданный матрицей смежности. A- матрица содержащая кратчайшие пути. P - матрица, сохраняющая маршруты. -------------------- Помогая друг другу, мы справимся с любыми трудностями!
"Не опускать крылья!" (С) |
| Altair |
 31.05.2005 7:01 31.05.2005 7:01
Сообщение
#3
|
 Ищущий истину       Группа: Модераторы Сообщений: 4 824 Пол: Мужской Реальное имя: Олег Репутация:  45 45  |
Поиск кратчайшего пути. Алгоритм Дейкстры
Процедура procedure Deikstr(n:integer; W:graph; u1,u2:integer; находит путь минимального веса в графе G, заданном весовой матрицей (матрица смежности) -W. При этом предполагается, что все элементы Wij неотрицательны. Путь ищется из вершины номер u1 к вершине номер u2 . Для представления веса, равного бесконечности (машинная бесконечность), используется число GM, передаваемое в алгоритм. Это число можно задавать в зависимости от конкретной задачи... модуль UNIT Dijkstra; демонстрационная программа компилятор BP7 (target windows) uses wincrt,dijkstra; В программе,граф считывается из файла. Вот для такого графа: 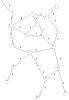 файл должен иметь вид (за машинную бесконечность берется 10000): Цитата 20 0 3 10000 10000 10000 10000 10000 10000 10000 10000 10000 10000 10000 10000 10000 10000 10000 10000 10000 10000 3 0 10000 10000 10000 3 10000 10000 10000 10000 10000 10000 10000 10000 10000 10000 10000 10000 10000 10000 10000 10000 0 2 10000 5 1 10000 10000 10000 10000 10000 10000 10000 10000 10000 10000 10000 10000 10000 10000 10000 2 0 3 10000 10000 5 10000 10000 10000 10000 10000 10000 10000 10000 10000 10000 10000 10000 10000 10000 10000 3 0 10000 10000 10000 10000 10000 10000 10000 10000 10000 10000 10000 10000 10000 10000 10000 10000 3 5 10000 10000 0 10000 10000 3 10000 10000 4 10000 10000 10000 10000 10000 10000 10000 10000 10000 10000 1 10000 10000 10000 0 10000 2 2 10000 10000 10000 10000 10000 10000 10000 10000 10000 10000 10000 10000 10000 5 10000 10000 10000 0 10000 10000 4 10000 10000 10000 10000 10000 10000 10000 10000 10000 10000 10000 10000 10000 10000 3 2 10000 0 2 10000 10000 10000 10000 10000 10000 10000 10000 10000 10000 10000 10000 10000 10000 10000 10000 2 10000 2 0 3 10000 10000 10000 10000 10000 10000 10000 10000 10000 10000 10000 10000 10000 10000 10000 10000 4 10000 3 0 10000 4 10000 10000 5 10000 10000 10000 10000 10000 10000 10000 10000 10000 4 10000 10000 10000 10000 10000 0 4 10000 10000 10000 10000 10000 10000 10000 10000 10000 10000 10000 10000 10000 10000 10000 10000 10000 4 4 0 4 3 10000 10000 10000 10000 10000 10000 10000 10000 10000 10000 10000 10000 10000 10000 10000 10000 10000 4 0 10000 10000 3 10000 10000 10000 10000 10000 10000 10000 10000 10000 10000 10000 10000 10000 10000 10000 3 10000 0 10000 10000 3 10000 10000 10000 10000 10000 10000 10000 10000 10000 10000 10000 10000 5 10000 10000 10000 10000 0 10000 4 7 10000 10000 10000 10000 10000 10000 10000 10000 10000 10000 10000 10000 10000 10000 3 10000 10000 0 10000 10000 10000 10000 10000 10000 10000 10000 10000 10000 10000 10000 10000 10000 10000 10000 10000 3 4 10000 0 10000 6 10000 10000 10000 10000 10000 10000 10000 10000 10000 10000 10000 10000 10000 10000 10000 7 10000 10000 0 10000 10000 10000 10000 10000 10000 10000 10000 10000 10000 10000 10000 10000 10000 10000 10000 10000 10000 6 10000 0 -------------------- Помогая друг другу, мы справимся с любыми трудностями!
"Не опускать крылья!" (С) |
| Altair |
 1.06.2005 21:56 1.06.2005 21:56
Сообщение
#4
|
 Ищущий истину       Группа: Модераторы Сообщений: 4 824 Пол: Мужской Реальное имя: Олег Репутация:  45 45  |
Эйлеров цикл.
Дадим теперь строгое определение эйлерову циклу и эйлерову графу. Если граф имеет цикл (не обязательно простой), содержащий все ребра графа по одному разу, то такой цикл называется эйлеровым циклом, а граф называется эйлеровым графом. Если граф имеет цепь (не обязательно простую), содержащую все вершины по одному разу, то такая цепь называется эйлеровой цепью, а граф называется полу-эйлеровым графом. Ясно, что эйлеров цикл содержит не только все ребра по одному разу, но и все вершины графа (возможно, по несколько раз). Очевидно также, что эйлеровым может быть только связный граф. Программа, строящая Эйлеров цикл, представленна ниже. (граф задается матрицей смежности, причем 0ставим если ребра нет, и один если есть). Uses CRT; -------------------- Помогая друг другу, мы справимся с любыми трудностями!
"Не опускать крылья!" (С) |
| Perfez |
 20.07.2007 17:07 20.07.2007 17:07
Сообщение
#5
|
 Бывалый    Группа: Модераторы Сообщений: 231 Пол: Женский Репутация:  6 6  |
Топологическая Сортировка Графа
Рассмотрим ациклический направленный граф содержащий N узлов (вершин). Топологической сортировкой узлов (также известной как RPO-нумерация или N-нумерация) ациклического графа называется алгоритм, присваивающий узлам графа номера от 1 до N таким образом, что все предшественники узла с номером M имеют номера меньше M. Граф , как обычно, задаётся смежным массивом. Алгоритм представляет собой простейшую модификацию алгоритма поиска в глубину, также указанной вверху (Смотри пост virt-а). Внизу представлена реализация Топологической Сортировки:
Сообщение отредактировано: Perfez - 21.07.2007 8:26 |
  |
3 чел. читают эту тему (гостей: 3, скрытых пользователей: 0)
Пользователей: 0

|
Текстовая версия | 16.11.2024 16:26 |








