Моделирование систем массового обслуживания Опции

[GoodWind]

МОДЕЛИРОВАНИЕ СИСТЕМ МАССОВОГО ОБСЛУЖИВАНИЯ
Основные понятия. Классификация СМО

При решении многих экономических задач, программист часто сталкивается с системами, выполняющими определенную работу, в которой нуждаются объекты, обращающиеся в эту систему (например: касса магазина, АЗС). Такие системы называют системами массового обслуживания (СМО), а обращающиеся объекты – заявками.

Элемент системы, в который поступают заявки, называют каналом или пунктом обслуживания. Соответственно, если в системе один канал, то систему называют одноканальной, если 2 или более – многоканальной.

На обслуживание одной заявки затрачивается определенное время, следовательно, в определенный момент времени на входе канала может либо находиться определенное количество заявок, либо вообще ни одной. В большинстве случаев предполагается, что известен некоторый вероятностный закон, управляющий поступлением заявок.

Цель решения СМО – минимизация затрат, связанных с простоем системы и затрат связанных с ожиданием заявок в очереди. СМО решается путем реформирования потоков заявок, либо определением оптимального количества каналов.

СМО делятся на два основные типа:

1. СМО с отказами:

требование, поступившее в момент, когда все каналы обслуживания заняты, получает отказ и покидает СМО не обслуженным. Пример – телефонная станция.

2. СМО ожиданием:

требование, поступившее в момент занятости всех каналов, становится в очередь и ожидает, когда освободится один из них. Пример – магазин, касса.

Основные компоненты СМО

Основными компонентами СМО являются:

1. Входной канал (прием заявок)
2. Система обслуживания
3. Очередь (для СМО с ожиданием)

Входной поток
Для входного потока предполагается, что известен средний интервал между заявками.
Интенсивностью входного потока (количество заявок за единицу времени) называют величину равную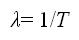

Величины λ и Т являются важными характеристиками входного потока. Величина Т определяет плотность потока, а λ — скорость поступления требований.

Функция плотности вероятности имеет вид:

а вероятность того, что за любой период Т поступит п требований вычисляется по формуле:

Все свойства и характеристики пуассоновского потока требований полностью определяются параметром λ.

Система обслуживания.
Любая система обслуживания состоит одного или нескольких каналов, каждый из которых затрачивает на обслуживание определенное время, но среднее время обслуживания считается у всех одинаковым и равным t.

Величина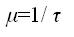

называется интенсивностью обслуживания. Она характеризует скорость работы канала и определяет среднее число требований, обслуживаемых каналом за единицу времени. Закон распределения обслуживания при одном и том же τ может быть различным, но чаще других встречается экспоненциальный закон. Функция плотности вероятности времени обслуживания имеет вид:


Очередь, дисциплина очереди
Ожидающие обслуживания заявки образуют очередь. Правила, по которым из очереди выбирают заявки для обслуживания называют дисциплиной очереди.
Различают 5 видов дисциплины:

1. FIFO – первой поступила – первой обслужена
2. LIFO – последней поступила – первой обслужена
3. По срочности
4. По приоритетам
5. Случайный выбор.

Сообщение отредактировано: GoodWind - 17.02.2006 21:35