 Компиляция правил для данного раздела
Компиляция правил для данного раздела
1. Заголовок темы должен быть информативным. В противном случае тема закрывается и удаляется ...
2. НЕ используйте форум для личного общения, все что не относится к обсуждению темы - на PM!
3. Одна тема - один вопрос (задача)
4. Спрашивайте и отвечайте четко и по существу!!!
| Кошка |
 29.09.2006 3:56 29.09.2006 3:56
Сообщение
#1
|
|
Группа: Пользователи Сообщений: 9 Пол: Женский Реальное имя: Светлана Репутация:  0 0  |
Помогите, плиз, решить задачи по доп. главам анализа
1. Док-ть, что кол-во всех пятёрок, которые можно нарисовать на плоскости (непересекающихся, разных размеров), - множество мощности континуума, а множество всех восьмёрок(непересекающихся) не более чем счётно 2. Док-ть, что множество всех непересекающихся следов(множеств трёх отрезков из одной точки) не более чем счётно 3. Пусть r1=1, r2n=rn +1, r(2n+1)=1/r2n, функция f из n в rn – биекция. Доказать, что функция f является биекцией из множества натуральных в множество рациональных чисел. |
  |
Ответов
| Lapp |
 29.09.2006 14:02 29.09.2006 14:02
Сообщение
#2
|
 Уникум        Группа: Модераторы Сообщений: 6 823 Пол: Мужской Реальное имя: Лопáрь (Андрей) Репутация:  159 159  |
Кошка,
не надо постить свои задачи в чужие темы - открывай новые. Задачи хорошие, ответы будут -------------------- я - ветер, я северный холодный ветер
я час расставанья, я год возвращенья домой |
| Lapp |
 2.10.2006 13:06 2.10.2006 13:06
Сообщение
#3
|
 Уникум        Группа: Модераторы Сообщений: 6 823 Пол: Мужской Реальное имя: Лопáрь (Андрей) Репутация:  159 159  |
1. Док-ть, что кол-во всех пятёрок, которые можно нарисовать на плоскости (непересекающихся, разных размеров), - множество мощности континуума, Вопрос по условию: пятерки должны быть подобны между собой? Если да, то при определенной форме пятерки доказательство, боюсь, невозможно. Поскольку в условии не определено точно, что есть пятерка, то будем считать, что они не обязательно должны быть подобны - главное, чтоб читались. Тогда решение состоит в построении примера, и пример я приведу для пятерок вполне определенной формы, которые все же подобны между собой (и даже равны). 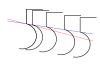 На рисунке самая левая пятерка - как бы первая, ее мы размножаем параллельным переносом вдоль синей линии. Синяя линия проходит немного горизонтальнее касательной к закруглению в месте сочленения (красная линия). Понятно, что такую пятерку можно провести через каждую точку синей линии, тем самым их множество равномощно множеству точек на прямой, которое есть континуум. Если касательная наклонена в другую сторону или горизонтальна, то такое решение не годится, но непольшой коррекцией формы мы все же можем добиться набора пятерок, которые будут вложены друг в друга достаточно плотно:  Продолжать процесс до такой степени, что пятерки будут плохо читаемыми, нет необходимости: между красной и синей их уже поместится континуум. Ну и вывод в обоих случаях следующий: мы нашли подмножество мощности континуум, само же множество не может превышать мощности континуум (каждой пятерке можно поставит в соответстие точку - например, край закругления). Следовательно множество пятерок континуально. а множество всех восьмёрок(непересекающихся) не более чем счётно Тут в некотором смысле проще, хотя рассуждений будет немного больше. Восьмерка в отличие от пятерки обладает площадью. Никакие предположения или ограничения на форму не нужны. Во-первых разобъем все действительные числа на полуинтервалы (1^n, 1^(n+1)], где n - любое целое число. Полуинтервал, в записи которого стоит число n, будем называть n-ым интервалом. Рассмотрим все восьмерки, у которых а) площадь находится в пределах n-ого интервала квадратных метров (далее единицы измерения опускаю); б) диаметр находится в пределах к-го интервала. Будем называть такие восьмерки (n,k)-восьмерками. Рассмотрим круг с центром в начале координат и радиусом равным максимальному диаметру (то есть 2^(k+1) ). В этот круг целиком может поместиться никак не более 2*S/(2^n) (n,k)-восьмерок (включая написанные внутри других таких же восьмерок; S - площадь круга), то есть конечное число. Теперь учтем те восьмерки, которые не вошли в круг полностью. Для этого окружим круг кольцом ширины 2^(k+1). Все они окажутся внутри большого круга, ограниченного внешней границей кольца. Это означает, что их тоже конечное число. Теперь увеличим радиус малого круга вдвое и повторим рассуждения. Таким образом, образовав бесконечную последовательность кругов, мы можем пересчитать все (n,k)-восьмерки. Тем самым мы доказали, что их множество счетно. Осталось только сказать, что количество классов (n,k)-восьмерок тоже счетно. А счетное объединение счетных множество также счетно. Тем самым задача о восьмерках решена. Задача о птичьих следах решается аналогично, с небольшой модификацией. Я напишу решение завтра (если никто не опередит -------------------- я - ветер, я северный холодный ветер
я час расставанья, я год возвращенья домой |
| Michael_Rybak |
 2.10.2006 14:16 2.10.2006 14:16
Сообщение
#4
|
|
Michael_Rybak      Группа: Модераторы Сообщений: 1 046 Пол: Мужской Реальное имя: Michael_Rybak Репутация:  32 32  |
Про восьмерки есть такое решение: поскольку множество рациональных чисел - счетно, то и множество точек с рациональными координатами - счетно, а, значит, счетно и множество *пар* точек с рациональными координатами. Выберем в каждом кругу восьмерки по точке с рац. координатами, и поставим эту пару ей в соответствие. Поскольку восьмерки не пересекаются, каждая пара может встретиться не больше одного раза.
Про птичьи следа - точно так же, только не пары, а тройки (соединяем концы отрезков, получаем треугольник, разбитый на три меньших следом. В каждом из меньших треугольников берем по рациональной точке). Хотя, в принципе, можно и двойками обойтись. Сообщение отредактировано: Michael_Rybak - 2.10.2006 14:24 |
| Lapp |
 2.10.2006 14:42 2.10.2006 14:42
Сообщение
#5
|
 Уникум        Группа: Модераторы Сообщений: 6 823 Пол: Мужской Реальное имя: Лопáрь (Андрей) Репутация:  159 159  |
каждая пара может встретиться не больше одного раза. Согласен. Ключ к решению - именно двусвязность, мое решение учитывает ее довольно сложным образом.. Про птичьи следа - точно так же, только не пары, а тройки (соединяем концы отрезков, получаем треугольник, разбитый на три меньших следом. В каждом из меньших треугольников берем по рациональной точке). Хотя, в принципе, можно и двойками обойтись. Боюсь, не годится.. Вот два следа и три рациональных точки, характеризующих каждый из них. Эскизы прикрепленных изображений 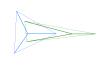
-------------------- я - ветер, я северный холодный ветер
я час расставанья, я год возвращенья домой |
| Michael_Rybak |
 2.10.2006 15:42 2.10.2006 15:42
Сообщение
#6
|
|
Michael_Rybak      Группа: Модераторы Сообщений: 1 046 Пол: Мужской Реальное имя: Michael_Rybak Репутация:  32 32  |
Да, вы правы. Я тут домучал до решения вроде, но даже не буду постить, т.к. так же изящно, как с восьмерками, не получилось (пока?).
|
| Lapp |
 3.10.2006 1:34 3.10.2006 1:34
Сообщение
#7
|
 Уникум        Группа: Модераторы Сообщений: 6 823 Пол: Мужской Реальное имя: Лопáрь (Андрей) Репутация:  159 159  |
Да, вы правы. Я тут домучал до решения вроде, но даже не буду постить, т.к. так же изящно, как с восьмерками, не получилось (пока?). Твое право - постить или не постить PS Спасибо за вклад в раздел! +1. -------------------- я - ветер, я северный холодный ветер
я час расставанья, я год возвращенья домой |
| Michael_Rybak |
 3.10.2006 17:34 3.10.2006 17:34
Сообщение
#8
|
|
Michael_Rybak      Группа: Модераторы Сообщений: 1 046 Пол: Мужской Реальное имя: Michael_Rybak Репутация:  32 32  |
Но если ничего лучшего все же не получится Получилось! Во-первых, будем рассматривать только следы, у которых все три отрезка равны - действительно, если бы удалось расположить континуум произвольных следов, то каждый след можно было бы обрезать до наименьшей из трех сторон, и получить континуум равносторонних следов. Поэтому, доказав счетность множества тех, покажем и счетность множества других. Будем называть длину отрезков радиусом. Во-вторых, будем рассматривать только следы с рациональным радиусом. Опять же, каждый след с иррациональным радиусом можно обрезать до рационального. А теперь зафиксируем радиус r, и применим критерий, который я приводил - три точки, по одной - в каждом треугольнике. Легко убедиться, что теперь Ваш пример (и аналогичные) построить нельзя. Значит, множество равносторонних следов одинакового рационального радиуса не более чем счетно, а, поскольку рациональных чисел - счетное количество, то и соответствующее декартово произведение (т.е. объединение следов всех радиусов) тоже не более чем счетно. |
| Lapp |
 4.10.2006 5:58 4.10.2006 5:58
Сообщение
#9
|
 Уникум        Группа: Модераторы Сообщений: 6 823 Пол: Мужской Реальное имя: Лопáрь (Андрей) Репутация:  159 159  |
Да, теперь лучше
Единственное мое замечание состоит в том, что вместо фразы: Легко убедиться, что теперь Ваш пример (и аналогичные) построить нельзя. - хотелось бы видеть некое геометрическое рассуждение с доказательством, а не ссылку на отсутствие гипотетических примеров. Думаю, ты согласишься.Мое решение в чем-то похоже (начало), в чем-то - нет (геометрия). Оно тоже использует усечение лучей до минимального. Потом я использовал разбиение на классы, как в решении для восьмерок - согласен, что усечение до рационального радиуса проще и красивее. Будем характеризовать каждый след его центром. Далее я использовал то свойство, что один из трех углов должен не превышать 120 градусов. Рассмотрим следы с близкими минимальными углами (аналогично классам в восьмерках, усечение угла до рационального, боюсь, тут не катит). Назовем это приближенное значение а. Поскольку второй (по величине) угол (назовем b) больше a, их сумма двух a. 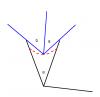 Таким образом, как видно из картинки, мы не можем расположить синий след (то есть его центр) ближе к черному следу, чем определяет некая граница (обозначена красным пунктиром). Значит, рядом с каждым (r,a)-следом находится некая "мертвая зона" фиксированной площади, в которой нету больше (r,a)-следов. Дальше понятно, полагаю.. -------------------- я - ветер, я северный холодный ветер
я час расставанья, я год возвращенья домой |
| Michael_Rybak |
 4.10.2006 12:00 4.10.2006 12:00
Сообщение
#10
|
|
Michael_Rybak      Группа: Модераторы Сообщений: 1 046 Пол: Мужской Реальное имя: Michael_Rybak Репутация:  32 32  |
хотелось бы видеть некое геометрическое рассуждение с доказательством, а не ссылку на отсутствие гипотетических примеров. Думаю, ты согласишься. Соглашусь Определимся более четко с тем, что такое след (равносторонний, с рациональным радиусом). След задается шестеркой (x, y, r, a1, a2, a3), где ai - углы, определяющие ветки. Из всех шестерок выбираем такую, в которой a1<a2<a3 В соответствие следу (x, y, r, a1, a2, a3) поставим шестерку рациональных чисел (x1, y1, x2, y2, x3, y3). Точку (x1, y1) выберем из сектора, ограниченного отрезками a1 и a2, причем не дальше от центра, чем на r/200. Аналогично выберем две другие точки из двух других секторов. Каждый след делит плоскость на три бесконечные части. Назовем каждую из них гранью следа. Теперь покажем, что двум непересекающимся следам с одинаковым радиусом не может соответствовать одна и та же шестерка. В противном случае понятно, что центры окружностей должны находится не дальше, чем на расстоянии r/100 друг от друга. А из этого следует, что каждый из следов обязательно полностью лежит в одной из граней другого. А это значит, с учетом близости центров, что из трех точек, которые мы поставим в соответствие одному следу, как минимум две будут лежать в одной грани другого. Поэтому совпадение шестерок невозможно. Извините что без рисунков, медленно они у меня получаются :-/ |
| Lapp |
 4.10.2006 13:04 4.10.2006 13:04
Сообщение
#11
|
 Уникум        Группа: Модераторы Сообщений: 6 823 Пол: Мужской Реальное имя: Лопáрь (Андрей) Репутация:  159 159  |
Ты согласен, что в цепочке рассуждений, являющих доказательство, все промежуточные выводы должны быть верными?
... А из этого следует, что каждый из следов обязательно полностью лежит в одной из граней другого. - ты настаиваешь?.. (руки чешутся нарисовать, но если ты предпочитаешь устно.. -------------------- я - ветер, я северный холодный ветер
я час расставанья, я год возвращенья домой |
Сообщений в этой теме
 Кошка Счетность, континуум, биекция 29.09.2006 3:56
Кошка Счетность, континуум, биекция 29.09.2006 3:56

 Michael_Rybak Вот елки :)
Ну чуть-чуть вылазить может :). Но у н... 4.10.2006 15:27
Michael_Rybak Вот елки :)
Ну чуть-чуть вылазить может :). Но у н... 4.10.2006 15:27

 lapp
Вот елки :)
O'kay, принято :) 5.10.2006 12:22
lapp
Вот елки :)
O'kay, принято :) 5.10.2006 12:22
 Michael_Rybak
3. Пусть r1=1, r2n=rn +1, r(2n+1)=1/r2n, функция ... 2.10.2006 14:40
Michael_Rybak
3. Пусть r1=1, r2n=rn +1, r(2n+1)=1/r2n, функция ... 2.10.2006 14:40
 Кошка Огромное спасибо за помощь! :respect2: 6.10.2006 20:29
Кошка Огромное спасибо за помощь! :respect2: 6.10.2006 20:29
 Гость помогите пожалуйста с вопросом-как доказать,что мн... 4.01.2010 19:25
Гость помогите пожалуйста с вопросом-как доказать,что мн... 4.01.2010 19:25
 andriano 0. Насколько мне известно, настоятельно рекомендуе... 4.01.2010 20:45
andriano 0. Насколько мне известно, настоятельно рекомендуе... 4.01.2010 20:45

 Lapp Гость, пожалуйста, зарегистрируйся и создавай свои... 5.01.2010 0:36
Lapp Гость, пожалуйста, зарегистрируйся и создавай свои... 5.01.2010 0:36

 andriano А как сводить? Было предложено 2 варианта.Можно и ... 5.01.2010 12:11
andriano А как сводить? Было предложено 2 варианта.Можно и ... 5.01.2010 12:11

 Lapp Сергей, это несерьезно..
Было предложено 2 вариант... 5.01.2010 23:31
Lapp Сергей, это несерьезно..
Было предложено 2 вариант... 5.01.2010 23:31

 andriano Доказательство требуется несомненно. Спираль абсо... 5.01.2010 23:57
andriano Доказательство требуется несомненно. Спираль абсо... 5.01.2010 23:57

 Lapp Мне кажется, ты придираешься.Я старался говорить т... 6.01.2010 0:18
Lapp Мне кажется, ты придираешься.Я старался говорить т... 6.01.2010 0:18

 andriano Хм.. Сейчас попробую.. Так. Схема с по крайней... 6.01.2010 0:30
andriano Хм.. Сейчас попробую.. Так. Схема с по крайней... 6.01.2010 0:30

 Lapp Это уже проба или она запланирована на дальнейшее?... 6.01.2010 0:42
Lapp Это уже проба или она запланирована на дальнейшее?... 6.01.2010 0:42

 andriano При чем тут счетность, я не знаю - спираль есть сп... 6.01.2010 12:29
andriano При чем тут счетность, я не знаю - спираль есть сп... 6.01.2010 12:29

 Lapp Можно аргументировать, почему не годится?Ну, я, вр... 6.01.2010 12:47
Lapp Можно аргументировать, почему не годится?Ну, я, вр... 6.01.2010 12:47
 Гость спс!!! :yes2: 5.01.2010 10:46
Гость спс!!! :yes2: 5.01.2010 10:46
 andriano У спирали должно быть ограничение на шаг (т.е. рас... 6.01.2010 13:16
andriano У спирали должно быть ограничение на шаг (т.е. рас... 6.01.2010 13:16
 Гость а можно попробовать установить соответствие с квад... 6.01.2010 20:53
Гость а можно попробовать установить соответствие с квад... 6.01.2010 20:53
 Lapp У спирали должно быть ограничение на шаг (т.е. рас... 6.01.2010 23:24
Lapp У спирали должно быть ограничение на шаг (т.е. рас... 6.01.2010 23:24

 andriano Во всяком случае, ты стойко не обращаешь внимания ... 6.01.2010 23:44
andriano Во всяком случае, ты стойко не обращаешь внимания ... 6.01.2010 23:44

 Lapp Я просто не знаю, что такое предельная точка. Не м... 7.01.2010 0:33
Lapp Я просто не знаю, что такое предельная точка. Не м... 7.01.2010 0:33

 andriano Допустим, мы пытаемся пересчитать их все по порядк... 7.01.2010 19:00
andriano Допустим, мы пытаемся пересчитать их все по порядк... 7.01.2010 19:00

 Lapp Ты не совсем верно представляешь себе, что такое с... 7.01.2010 23:39
Lapp Ты не совсем верно представляешь себе, что такое с... 7.01.2010 23:39
 andriano Нет, ничего стирать я не буду.
Если я написал глуп... 8.01.2010 15:48
andriano Нет, ничего стирать я не буду.
Если я написал глуп... 8.01.2010 15:48

 Lapp По всей видимости, мы говорим на разных языках.
Я ... 9.01.2010 0:27
Lapp По всей видимости, мы говорим на разных языках.
Я ... 9.01.2010 0:27

 Lapp Гоп-стоп! Я полез проверять фразу andriano:
... 9.01.2010 1:18
Lapp Гоп-стоп! Я полез проверять фразу andriano:
... 9.01.2010 1:18
 Lapp Итак, попытаюсь выполнить обещание )).
Собственно,... 9.01.2010 23:59
Lapp Итак, попытаюсь выполнить обещание )).
Собственно,... 9.01.2010 23:59

 Lapp Про использование спирали во второй задаче я напиш... 10.01.2010 4:12
Lapp Про использование спирали во второй задаче я напиш... 10.01.2010 4:12

 andriano А именно:Можно уточнить, что именно мы доказываем... 10.01.2010 15:40
andriano А именно:Можно уточнить, что именно мы доказываем... 10.01.2010 15:40

 Lapp Конечно. Я доказываю гипотезу, что множество всех... 11.01.2010 3:23
Lapp Конечно. Я доказываю гипотезу, что множество всех... 11.01.2010 3:23
 andriano Убедил.
Первоначально я невнимательно прочел вопро... 10.01.2010 16:01
andriano Убедил.
Первоначально я невнимательно прочел вопро... 10.01.2010 16:01
 andriano 1-я задача из 16-го поста. Теперь понятно. 11.01.2010 20:29
andriano 1-я задача из 16-го поста. Теперь понятно. 11.01.2010 20:29
 Lapp 1-я задача из 16-го поста. Теперь понятно.Ваша нев... 11.01.2010 23:57
Lapp 1-я задача из 16-го поста. Теперь понятно.Ваша нев... 11.01.2010 23:57
 andriano Правила хорошего тона на Интернет-форумах настояте... 12.01.2010 20:15
andriano Правила хорошего тона на Интернет-форумах настояте... 12.01.2010 20:15
 Lapp Правила хорошего тона на Интернет-форумах настояте... 13.01.2010 5:37
Lapp Правила хорошего тона на Интернет-форумах настояте... 13.01.2010 5:37  |
1 чел. читают эту тему (гостей: 1, скрытых пользователей: 0)
Пользователей: 0

|
Текстовая версия | 9.12.2025 6:15 |









