 Компиляция правил для данного раздела
Компиляция правил для данного раздела
1. Заголовок темы должен быть информативным. В противном случае тема закрывается и удаляется ...
2. НЕ используйте форум для личного общения, все что не относится к обсуждению темы - на PM!
3. Одна тема - один вопрос (задача)
4. Спрашивайте и отвечайте четко и по существу!!!
| Кошка |
 29.09.2006 3:56 29.09.2006 3:56
Сообщение
#1
|
|
Группа: Пользователи Сообщений: 9 Пол: Женский Реальное имя: Светлана Репутация:  0 0  |
Помогите, плиз, решить задачи по доп. главам анализа
1. Док-ть, что кол-во всех пятёрок, которые можно нарисовать на плоскости (непересекающихся, разных размеров), - множество мощности континуума, а множество всех восьмёрок(непересекающихся) не более чем счётно 2. Док-ть, что множество всех непересекающихся следов(множеств трёх отрезков из одной точки) не более чем счётно 3. Пусть r1=1, r2n=rn +1, r(2n+1)=1/r2n, функция f из n в rn – биекция. Доказать, что функция f является биекцией из множества натуральных в множество рациональных чисел. |
  |
Ответов
| Lapp |
 29.09.2006 14:02 29.09.2006 14:02
Сообщение
#2
|
 Уникум        Группа: Модераторы Сообщений: 6 823 Пол: Мужской Реальное имя: Лопáрь (Андрей) Репутация:  159 159  |
Кошка,
не надо постить свои задачи в чужие темы - открывай новые. Задачи хорошие, ответы будут -------------------- я - ветер, я северный холодный ветер
я час расставанья, я год возвращенья домой |
| Lapp |
 2.10.2006 13:06 2.10.2006 13:06
Сообщение
#3
|
 Уникум        Группа: Модераторы Сообщений: 6 823 Пол: Мужской Реальное имя: Лопáрь (Андрей) Репутация:  159 159  |
1. Док-ть, что кол-во всех пятёрок, которые можно нарисовать на плоскости (непересекающихся, разных размеров), - множество мощности континуума, Вопрос по условию: пятерки должны быть подобны между собой? Если да, то при определенной форме пятерки доказательство, боюсь, невозможно. Поскольку в условии не определено точно, что есть пятерка, то будем считать, что они не обязательно должны быть подобны - главное, чтоб читались. Тогда решение состоит в построении примера, и пример я приведу для пятерок вполне определенной формы, которые все же подобны между собой (и даже равны). 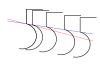 На рисунке самая левая пятерка - как бы первая, ее мы размножаем параллельным переносом вдоль синей линии. Синяя линия проходит немного горизонтальнее касательной к закруглению в месте сочленения (красная линия). Понятно, что такую пятерку можно провести через каждую точку синей линии, тем самым их множество равномощно множеству точек на прямой, которое есть континуум. Если касательная наклонена в другую сторону или горизонтальна, то такое решение не годится, но непольшой коррекцией формы мы все же можем добиться набора пятерок, которые будут вложены друг в друга достаточно плотно:  Продолжать процесс до такой степени, что пятерки будут плохо читаемыми, нет необходимости: между красной и синей их уже поместится континуум. Ну и вывод в обоих случаях следующий: мы нашли подмножество мощности континуум, само же множество не может превышать мощности континуум (каждой пятерке можно поставит в соответстие точку - например, край закругления). Следовательно множество пятерок континуально. а множество всех восьмёрок(непересекающихся) не более чем счётно Тут в некотором смысле проще, хотя рассуждений будет немного больше. Восьмерка в отличие от пятерки обладает площадью. Никакие предположения или ограничения на форму не нужны. Во-первых разобъем все действительные числа на полуинтервалы (1^n, 1^(n+1)], где n - любое целое число. Полуинтервал, в записи которого стоит число n, будем называть n-ым интервалом. Рассмотрим все восьмерки, у которых а) площадь находится в пределах n-ого интервала квадратных метров (далее единицы измерения опускаю); б) диаметр находится в пределах к-го интервала. Будем называть такие восьмерки (n,k)-восьмерками. Рассмотрим круг с центром в начале координат и радиусом равным максимальному диаметру (то есть 2^(k+1) ). В этот круг целиком может поместиться никак не более 2*S/(2^n) (n,k)-восьмерок (включая написанные внутри других таких же восьмерок; S - площадь круга), то есть конечное число. Теперь учтем те восьмерки, которые не вошли в круг полностью. Для этого окружим круг кольцом ширины 2^(k+1). Все они окажутся внутри большого круга, ограниченного внешней границей кольца. Это означает, что их тоже конечное число. Теперь увеличим радиус малого круга вдвое и повторим рассуждения. Таким образом, образовав бесконечную последовательность кругов, мы можем пересчитать все (n,k)-восьмерки. Тем самым мы доказали, что их множество счетно. Осталось только сказать, что количество классов (n,k)-восьмерок тоже счетно. А счетное объединение счетных множество также счетно. Тем самым задача о восьмерках решена. Задача о птичьих следах решается аналогично, с небольшой модификацией. Я напишу решение завтра (если никто не опередит -------------------- я - ветер, я северный холодный ветер
я час расставанья, я год возвращенья домой |
Сообщений в этой теме
 Кошка Счетность, континуум, биекция 29.09.2006 3:56
Кошка Счетность, континуум, биекция 29.09.2006 3:56

 Michael_Rybak Про восьмерки есть такое решение: поскольку множес... 2.10.2006 14:16
Michael_Rybak Про восьмерки есть такое решение: поскольку множес... 2.10.2006 14:16

 lapp
каждая пара может встретиться не больше одного ра... 2.10.2006 14:42
lapp
каждая пара может встретиться не больше одного ра... 2.10.2006 14:42

 Michael_Rybak Да, вы правы. Я тут домучал до решения вроде, но д... 2.10.2006 15:42
Michael_Rybak Да, вы правы. Я тут домучал до решения вроде, но д... 2.10.2006 15:42

 lapp
Да, вы правы. Я тут домучал до решения вроде, но ... 3.10.2006 1:34
lapp
Да, вы правы. Я тут домучал до решения вроде, но ... 3.10.2006 1:34

 Michael_Rybak
Но если ничего лучшего все же не получится
Полу... 3.10.2006 17:34
Michael_Rybak
Но если ничего лучшего все же не получится
Полу... 3.10.2006 17:34

 lapp Да, теперь лучше :).
Единственное мое замечание со... 4.10.2006 5:58
lapp Да, теперь лучше :).
Единственное мое замечание со... 4.10.2006 5:58

 Michael_Rybak
хотелось бы видеть некое геометрическое рассужден... 4.10.2006 12:00
Michael_Rybak
хотелось бы видеть некое геометрическое рассужден... 4.10.2006 12:00

 lapp Ты согласен, что в цепочке рассуждений, являющих д... 4.10.2006 13:04
lapp Ты согласен, что в цепочке рассуждений, являющих д... 4.10.2006 13:04

 Michael_Rybak Вот елки :)
Ну чуть-чуть вылазить может :). Но у н... 4.10.2006 15:27
Michael_Rybak Вот елки :)
Ну чуть-чуть вылазить может :). Но у н... 4.10.2006 15:27

 lapp
Вот елки :)
O'kay, принято :) 5.10.2006 12:22
lapp
Вот елки :)
O'kay, принято :) 5.10.2006 12:22
 Michael_Rybak
3. Пусть r1=1, r2n=rn +1, r(2n+1)=1/r2n, функция ... 2.10.2006 14:40
Michael_Rybak
3. Пусть r1=1, r2n=rn +1, r(2n+1)=1/r2n, функция ... 2.10.2006 14:40
 Кошка Огромное спасибо за помощь! :respect2: 6.10.2006 20:29
Кошка Огромное спасибо за помощь! :respect2: 6.10.2006 20:29
 Гость помогите пожалуйста с вопросом-как доказать,что мн... 4.01.2010 19:25
Гость помогите пожалуйста с вопросом-как доказать,что мн... 4.01.2010 19:25
 andriano 0. Насколько мне известно, настоятельно рекомендуе... 4.01.2010 20:45
andriano 0. Насколько мне известно, настоятельно рекомендуе... 4.01.2010 20:45

 Lapp Гость, пожалуйста, зарегистрируйся и создавай свои... 5.01.2010 0:36
Lapp Гость, пожалуйста, зарегистрируйся и создавай свои... 5.01.2010 0:36

 andriano А как сводить? Было предложено 2 варианта.Можно и ... 5.01.2010 12:11
andriano А как сводить? Было предложено 2 варианта.Можно и ... 5.01.2010 12:11

 Lapp Сергей, это несерьезно..
Было предложено 2 вариант... 5.01.2010 23:31
Lapp Сергей, это несерьезно..
Было предложено 2 вариант... 5.01.2010 23:31

 andriano Доказательство требуется несомненно. Спираль абсо... 5.01.2010 23:57
andriano Доказательство требуется несомненно. Спираль абсо... 5.01.2010 23:57

 Lapp Мне кажется, ты придираешься.Я старался говорить т... 6.01.2010 0:18
Lapp Мне кажется, ты придираешься.Я старался говорить т... 6.01.2010 0:18

 andriano Хм.. Сейчас попробую.. Так. Схема с по крайней... 6.01.2010 0:30
andriano Хм.. Сейчас попробую.. Так. Схема с по крайней... 6.01.2010 0:30

 Lapp Это уже проба или она запланирована на дальнейшее?... 6.01.2010 0:42
Lapp Это уже проба или она запланирована на дальнейшее?... 6.01.2010 0:42

 andriano При чем тут счетность, я не знаю - спираль есть сп... 6.01.2010 12:29
andriano При чем тут счетность, я не знаю - спираль есть сп... 6.01.2010 12:29

 Lapp Можно аргументировать, почему не годится?Ну, я, вр... 6.01.2010 12:47
Lapp Можно аргументировать, почему не годится?Ну, я, вр... 6.01.2010 12:47
 Гость спс!!! :yes2: 5.01.2010 10:46
Гость спс!!! :yes2: 5.01.2010 10:46
 andriano У спирали должно быть ограничение на шаг (т.е. рас... 6.01.2010 13:16
andriano У спирали должно быть ограничение на шаг (т.е. рас... 6.01.2010 13:16
 Гость а можно попробовать установить соответствие с квад... 6.01.2010 20:53
Гость а можно попробовать установить соответствие с квад... 6.01.2010 20:53
 Lapp У спирали должно быть ограничение на шаг (т.е. рас... 6.01.2010 23:24
Lapp У спирали должно быть ограничение на шаг (т.е. рас... 6.01.2010 23:24

 andriano Во всяком случае, ты стойко не обращаешь внимания ... 6.01.2010 23:44
andriano Во всяком случае, ты стойко не обращаешь внимания ... 6.01.2010 23:44

 Lapp Я просто не знаю, что такое предельная точка. Не м... 7.01.2010 0:33
Lapp Я просто не знаю, что такое предельная точка. Не м... 7.01.2010 0:33

 andriano Допустим, мы пытаемся пересчитать их все по порядк... 7.01.2010 19:00
andriano Допустим, мы пытаемся пересчитать их все по порядк... 7.01.2010 19:00

 Lapp Ты не совсем верно представляешь себе, что такое с... 7.01.2010 23:39
Lapp Ты не совсем верно представляешь себе, что такое с... 7.01.2010 23:39
 andriano Нет, ничего стирать я не буду.
Если я написал глуп... 8.01.2010 15:48
andriano Нет, ничего стирать я не буду.
Если я написал глуп... 8.01.2010 15:48

 Lapp По всей видимости, мы говорим на разных языках.
Я ... 9.01.2010 0:27
Lapp По всей видимости, мы говорим на разных языках.
Я ... 9.01.2010 0:27

 Lapp Гоп-стоп! Я полез проверять фразу andriano:
... 9.01.2010 1:18
Lapp Гоп-стоп! Я полез проверять фразу andriano:
... 9.01.2010 1:18
 Lapp Итак, попытаюсь выполнить обещание )).
Собственно,... 9.01.2010 23:59
Lapp Итак, попытаюсь выполнить обещание )).
Собственно,... 9.01.2010 23:59

 Lapp Про использование спирали во второй задаче я напиш... 10.01.2010 4:12
Lapp Про использование спирали во второй задаче я напиш... 10.01.2010 4:12

 andriano А именно:Можно уточнить, что именно мы доказываем... 10.01.2010 15:40
andriano А именно:Можно уточнить, что именно мы доказываем... 10.01.2010 15:40

 Lapp Конечно. Я доказываю гипотезу, что множество всех... 11.01.2010 3:23
Lapp Конечно. Я доказываю гипотезу, что множество всех... 11.01.2010 3:23
 andriano Убедил.
Первоначально я невнимательно прочел вопро... 10.01.2010 16:01
andriano Убедил.
Первоначально я невнимательно прочел вопро... 10.01.2010 16:01
 andriano 1-я задача из 16-го поста. Теперь понятно. 11.01.2010 20:29
andriano 1-я задача из 16-го поста. Теперь понятно. 11.01.2010 20:29
 Lapp 1-я задача из 16-го поста. Теперь понятно.Ваша нев... 11.01.2010 23:57
Lapp 1-я задача из 16-го поста. Теперь понятно.Ваша нев... 11.01.2010 23:57
 andriano Правила хорошего тона на Интернет-форумах настояте... 12.01.2010 20:15
andriano Правила хорошего тона на Интернет-форумах настояте... 12.01.2010 20:15
 Lapp Правила хорошего тона на Интернет-форумах настояте... 13.01.2010 5:37
Lapp Правила хорошего тона на Интернет-форумах настояте... 13.01.2010 5:37  |
1 чел. читают эту тему (гостей: 1, скрытых пользователей: 0)
Пользователей: 0

|
Текстовая версия | 9.12.2025 6:14 |









