| GreyWind |
 29.08.2006 11:05 29.08.2006 11:05
Сообщение
#1
|
|
Гость |
Подскажите пожалуйста с чего начать решение этих задач... Все таки хочется их самому решить, но нет ни одной мысли
1)В вершинах правильного шестиугольника со стороной a расположены точечные заряды q,2q,3q,4q,5q,6q. Найти силу действующую на точечный заряд q лежащий на пересечении диагоналей шестиугольника? 2)N одинакавых шарообразных одноименно заряженных капелек ртути имеют один и тот же потенциал. Каков будет потенциал большой капли ртути получившейся в результате слияния этих капель? Исходя из суперпозиции потенциалов должно быть ф1+ф2+ф3+...+фN... Но насколько я понимаю это слишком просто... 3)Два металических шара расположенные далеко друг от друга имеют радиусы 5см 15см и заряды 12нКл и -40нКл. Шары соединяют тонкой проволокой. Какой заряд дельта q пройдет по проволоке? |
  |
Ответов
| Clerick |
 30.08.2006 15:51 30.08.2006 15:51
Сообщение
#2
|
 студент..    Группа: Пользователи Сообщений: 287 Пол: Мужской Реальное имя: Дмитрий Репутация:  2 2  |
To Lapp, по поводу второй, виноват, забыл. Имел в виду что заряд для потенциала большой капли Q=Nq. По поводу третьей, думаю можно обьяснить так: проводник насколько тонкий, что его электроемкостью можно пренебречь => зарядом на нем тоже можно пренебречь. Или так нельзя
Сообщение отредактировано: Clerick - 30.08.2006 15:52 -------------------- После дождя обязательно выглянет солнце)
|
| Lapp |
 31.08.2006 5:54 31.08.2006 5:54
Сообщение
#3
|
 Уникум        Группа: Модераторы Сообщений: 6 823 Пол: Мужской Реальное имя: Лопáрь (Андрей) Репутация:  159 159  |
[b]По поводу третьей, думаю можно обьяснить так: проводник насколько тонкий, что его электроемкостью можно пренебречь => зарядом на нем тоже можно пренебречь. Или так нельзя Я имел в виду следующее: картины поля вокруг системы из двух шаров без проволоки (то есть таких, для которых работают формулы потенциала) и с проволокой между ними довольно разные (см рисунок). 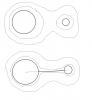 Близкие к поверхностям шаров эквипотенциали в первом случае представляют собой почти круги - или по крайней мере два отдельных замкнутых контура, а во втором случае все - как далекие от поверхности так и близкие к ней эквипотенциали имеют форму гантели. Я не могу сказать на вскидку, чем это может грозить, но думаю, что "очень тонкого" провода в этом смысле не существует - даже провод нудевой толщины внесет подобные искажения. Конечно, его можно потом убрать, но для этого его нужно разомкнуть, чем прекратить переток зарядов, и конечный заряд может все же быть не таким, как для двух эквипотенциальных сфер.. Точнее сказать сейчас не могу, подумаю еще. -------------------- я - ветер, я северный холодный ветер
я час расставанья, я год возвращенья домой |
| Clerick |
 31.08.2006 15:30 31.08.2006 15:30
Сообщение
#4
|
 студент..    Группа: Пользователи Сообщений: 287 Пол: Мужской Реальное имя: Дмитрий Репутация:  2 2  |
Я имел в виду...<>. Нет, конечно, я абсолютно согласен с тобой! Тут даже никаких сомнений не возникает, что эквипотенциальные поверхности - это "гантели", но тогда решение получается гораздо сложнее... Лично, у нас в школе учительница физики так и обьяснила это явление. Именно так: "Электроемкостью провода пренебрегаем...". Естественно это сделано для упрощения задачи, но так же упрощаются школьные задачи по механике, к примеру, "сопротивлением воздуха пренебречь". А вот если к задаче добавить еще одно условие "шары находятся на большом расстоянии друг от друга"? Тогда в принципе можно считать эквипотенциальные поверхности приближенными к круговым, хотя можно ли? To GreyWind обращайся! Сообщение отредактировано: Clerick - 31.08.2006 15:31 -------------------- После дождя обязательно выглянет солнце)
|
Сообщений в этой теме
 GreyWind Задачи по электростатике 29.08.2006 11:05
GreyWind Задачи по электростатике 29.08.2006 11:05
 Clerick 1. Сделай хороший рисунок, нарисуй каждую силу и с... 29.08.2006 16:01
Clerick 1. Сделай хороший рисунок, нарисуй каждую силу и с... 29.08.2006 16:01
 GreyWind Большое спасибо за помощь!!! Пойду поп... 30.08.2006 11:50
GreyWind Большое спасибо за помощь!!! Пойду поп... 30.08.2006 11:50

 lapp Clerick, первую задачу можно решить устно. Рассмо... 30.08.2006 13:06
lapp Clerick, первую задачу можно решить устно. Рассмо... 30.08.2006 13:06
 GreyWind С первой и второй задачкой вроде все понятно... А ... 31.08.2006 11:06
GreyWind С первой и второй задачкой вроде все понятно... А ... 31.08.2006 11:06

 lapp
В ответе должно получиться 25нКл. Подскажите что ... 31.08.2006 11:27
lapp
В ответе должно получиться 25нКл. Подскажите что ... 31.08.2006 11:27
 GreyWind Наверное в задачнике действительно ошибка. Услови... 31.08.2006 11:49
GreyWind Наверное в задачнике действительно ошибка. Услови... 31.08.2006 11:49  |
1 чел. читают эту тему (гостей: 1, скрытых пользователей: 0)
Пользователей: 0

|
Текстовая версия | 15.11.2025 16:09 |









