 Компиляция правил для данного раздела
Компиляция правил для данного раздела
1. Заголовок темы должен быть информативным. В противном случае тема закрывается и удаляется ...
2. НЕ используйте форум для личного общения, все что не относится к обсуждению темы - на PM!
3. Одна тема - один вопрос (задача)
4. Спрашивайте и отвечайте четко и по существу!!!
| Dead.MorozZ |
 23.02.2006 22:52 23.02.2006 22:52
Сообщение
#1
|
|
Пионер   Группа: Пользователи Сообщений: 108 Пол: Мужской Реальное имя: Георгий Репутация:  0 0  |
Помогите решить задачу или подскажите идею!
Через центр O окружности X описаной около треугольника ABC, проведена прямая, параллельная BC и пересекающая стороны AB и AC в точках B1, C1 соответственно. Окружность Y проходит через точки B1, C1 и кисается окружности X в точке K. Найти угол между прямыми AK и BC. Найти площадь треугольника ABC и радиус окружности X если BC = 9 AK = 8 B1C1 =6. Сообщение отредактировано: Dead.MorozZ - 23.02.2006 22:53 -------------------- Минус - это уже половина плюса, а плюс порой - целых два минуса...
|
  |
Ответов
| Lapp |
 24.02.2006 6:16 24.02.2006 6:16
Сообщение
#2
|
 Уникум        Группа: Модераторы Сообщений: 6 823 Пол: Мужской Реальное имя: Лопáрь (Андрей) Репутация:  159 159  |
Когда нарисуем все, кроме окружности Y, станет ясно, что окружностей, проходящих через B' и C' и касающихся X, можно провести две. Одна из них касается Х в верхней части, другая - в нижней. Возникает вопрос: какая из них имелась в виду? Для ответа исследуем ситуацию.
Пока не будем проводить окружность Y (ни сверху, ни снизу), а вместо этого опишем окружность (назовем ее Z) вокруг тр.AB'C' (на рисунке она красная). Поскольку этот треугольник подобен тр.АВС с центром подобия в А, то и окружность Z подобна Х, а ее центр лежит на отрезке ОА. Но ОА - это радиус окр.Х, и окр.Z проходит через А. Это означает, что Z касается Х в точке А. Таким образом, Z оказалась одним из возможных воплощений Y. Но Z касается X в точке А, то есть расстояние от А до точки касания равно нулю, а по условию оно равно 8. Следовательно, окружность Y должна касаться Х снизу. Посмотрев на рисунок, легко прийти к выводу, что Y является симметричной к Z относительно B'C'. На этом посторение заканчивается, и начинаются расчеты.. Из симметрии заключаем, что АК перпендикулярна B'C' и делится ей пополам (в т. М): АМ=4. Из подобия находим АN = АМ * (BC/B'C') = 4*(9/6) = 6 . Плошадь тр.АВС равна 0.5*9*6 = 27 . Все. PS Красивая задачка, понравилась.. Спасибо! Дед, откуда ты их берешь? Сообщение отредактировано: lapp - 24.02.2006 8:00 Эскизы прикрепленных изображений 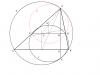
-------------------- я - ветер, я северный холодный ветер
я час расставанья, я год возвращенья домой |
Сообщений в этой теме
 Dead.MorozZ Описанная окружность 23.02.2006 22:52
Dead.MorozZ Описанная окружность 23.02.2006 22:52
 Dead.MorozZ
:good: ЗФТШ :good:
Там еще столько "кра... 24.02.2006 18:34
Dead.MorozZ
:good: ЗФТШ :good:
Там еще столько "кра... 24.02.2006 18:34
 lapp
Буду тебя по-чаще радовать :) :)
почаще - ок? ... 25.02.2006 7:20
lapp
Буду тебя по-чаще радовать :) :)
почаще - ок? ... 25.02.2006 7:20  |
1 чел. читают эту тему (гостей: 1, скрытых пользователей: 0)
Пользователей: 0

|
Текстовая версия | 27.07.2025 8:06 |









