графы, алгоритмы на графах Опции

[virt]

Графы можно представлять в виде множества вершин и множества соединяющих их ребер. (Города и дороги их соединяющие)

1. Просмотр вершин графа в некотором фиксированном порядке.

общие структуры данных :

const Maxn=100;
var a:array[1..Maxn,1..Maxn]of integer;
    Nnew:array[1..Maxn]of boolean;
    n,i,j:integer;

поиск в глубину :

{ рекурсивный вариант }
procedure Pg(v:integer);
var i:integer;
begin
   Nnew[v]:=false;
   write(v:2);
   for i:=1 to n do
      if (a[v,i]<>0) and Nnew[i] then Pg(i);
end;

{ нерекурсивный вариант }
procedure Pg_nonrec(v:integer);
var St:array[1..Maxn]of integer;
    yk:integer;
    t,j:integer;
    pp:boolean;
begin
   fillchar(St,sizeof(St),0);
   yk:=1;
   St[yk]:=v;Nnew[v]:=false;
   write(v:2);
   while yk <> 0 do
      begin
         t:=St[yk];j:=0;pp:=false;
         repeat
            if (a[t,j+1] <> 0) and Nnew[j+1] then pp:=true
               else inc(j);
         until pp or (j >= n);
         if pp then
            begin
               inc(yk);St[yk]:=j+1;Nnew[j+1]:=false;
               write(j+1:2);
            end else
               dec(yk);
      end;
end;

Поиск в ширину:

procedure Pw(v:integer);
var Og:array[1..Maxn]of 0..Maxn;
    yk1,yk2:integer;
    j:integer;
begin
   fillchar(Og,sizeof(Og),0);yk2:=0;
   yk1:=1;Og[yk1]:=v;Nnew[v]:=false;
   while yk2 < yk1 do
      begin
         inc(yk2);v:=Og[yk2];
         write(v:2);
         for j:=1 to n do
            if (a[v,j] <> 0) and Nnew[j] then
               begin
                  inc(yk1);Og[yk1]:=j;Nnew[j]:=false;
               end;
      end;
end;

2. Каркасы (стягивающие деревья)

const Maxn=100;
var a:array[1..Maxn,1..Maxn]of byte;
    Nnew:array[1..Maxn]of boolean;
    Tree:array[1..2,1..Maxn]of integer;
    n,i,j:integer;
    yk:integer;

Построение стягивающего дерева поиском в глубину:

procedure Tree_Depth(v:integer);
var i:integer;
begin
   Nnew[v]:=false;
   for i:=1 to n do
      if (a[v,i] <> 0) and Nnew[i] then
         begin
            inc(yk);Tree[1,yk]:=v;Tree[2,yk]:=i;
            Tree_Depth(i);
         end;
end;

Построение стягивающего дерева поиском в ширину:

procedure Tree_Width(v:integer);
var Turn:array[1..Maxn]of integer;
    yr,yw,i:integer;
begin
   fillchar(Turn,sizeof(Turn),0);yr:=0;
   yw:=1;Turn[yw]:=v;Nnew[v]:=false;
   while yw <> yr do
      begin
         inc(yr);v:=Turn[yr];
         for i:=1 to n do
            if (a[i,j] <> 0) and Nnew[i] then
               begin
                  inc(yw);Turn[yw]:=i;Nnew[i]:=false;
                  inc(yk);Tree[1,yk]:=v;Tree[2,yk]:=i;
               end;
      end;
end;

Построение всех каркасов графа:

const Maxn=100;
var a:array[1..Maxn,1..Maxn]of byte;
    Nnew:array[1..Maxn]of boolean;
    Tree:array[1..2,1..Maxn]of integer;
    Turn:array[1..maxn]of integer;
    n,i,j:integer;
    numb:integer;
    down,up:integer;

..............

procedure solve(v,q:integer);
var j:integer;
begin
   if down >= up then exit;
   j:=q;
   while (j <= n) and (numb < n-1) do
       begin
          if (a[v,j] <> 0) and Nnew[j] then
             begin
                Nnew[j]:=false;
                inc(numb);
                Tree[1,numb]:=v;Tree[2,numb]:=j;
                Turn[up]:=j;inc(up);
                solve(v,j+1);
                dec(up);Nnew[j]:=true;dec(numb);
             end;
          inc(j);
       end;
   if numb = n-1 then
      begin
         writeln;
         for i:=1 to numb do
            write(Tree[1,i],' ',Tree[2,i],'  ');
         exit;
      end;
   if j = n+1 then
      begin
         inc(down);
         solve(Turn[down],1);
         dec(down);
      end;
end;

Построение минимального каркаса методом Краскала:
(Исправлено. Присоединенный архив перезалит)

Граф задан списком ребер с указанием их весов:

program minim_tree_kraskal;
const maxn=100;
var p:array[1..3,1..maxn*(maxn-1) div 2]of integer;
    Mark:array[1..maxn]of integer;
    k,i,t:integer;
    m,n:integer;{m - rebra;n - vershini }

procedure Change_Mark(l,m:integer);
var i,t:integer;
begin
   if m < l then
      begin
         t:=l;l:=m;m:=t;
      end;
   for i:=1 to n do
      if Mark[i]=m then Mark[i]:=l;
end;

begin
   readln(n,m);
   for i:=1 to m do
      read(p[1,i],p[2,i],p[3,i]);
   for i:=1 to m-1 do
      for t:=i+1 to m do
         if p[3,i] > p[3,t] then
            begin
               k:=p[1,i];p[1,i]:=p[1,t];p[1,t]:=k;
               k:=p[2,i];p[2,i]:=p[2,t];p[2,t]:=k;
               k:=p[3,i];p[3,i]:=p[3,t];p[3,t]:=k;
            end;
   for i:=1 to n do mark[i]:=i;
   k:=0;t:=m;
   while k < n-1 do
      begin
         i:=1;
         while (i <= t) and (Mark[p[1,i]] = Mark[p[2,i]]) and (p[1,i] <> 0) do inc(i);
         inc(k);

         if p[1, i] * p[2, i] <> 0 then begin { Добавлена проверка на ненулевые вершины }
            write(p[1,i],' ',p[2,i],'  ');
            change_Mark(Mark[p[1,i]],Mark[p[2,i]]);
         end;
      end;
end.

Построение минимального каркаса методом Прима:

procedure solve;
var sm,sp:set of 1..maxn;
    min,i,j,l,t:integer;
begin
   min:=maxint;
   sm:=[1..n];sp:=[];
   for i:=1 to n-1 do
      for j:=i+1 to n do
         if (a[i,j] < min) and (a[i,j] <> 0) then
            begin
               min:=a[i,j];
               l:=i;t:=j;
            end;
   sp:=[l,t];sm:=sm-[l,t];
   write(l,' ',t ,'  ');
   while sm <> [] do
      begin
         min:=maxint;
         l:=0;t:=0;
         for i:=1 to n do
            if not (i in sp) then
               for j:=1 to n do
                  if (j in sp) and (a[i,j] < min) and (a[i,j] <> 0) then
                     begin
                        min:=a[i,j];
                        l:=i;t:=j;
                     end;
         sp:=sp+[l];sm:=sm-[l];
         write(l,' ',t,'  ');
      end;
end;

Сообщение отредактировано: volvo - 13.01.2009 11:36

[Altair]

Поиск кратчайшего пути. Алгоритм Дейкстры
Процедура

procedure Deikstr(n:integer; W:graph; u1,u2:integer;
                  var length:integer; var Weight:real; var Path: array of integer);

находит путь минимального веса в графе G, заданном весовой матрицей (матрица смежности) -W.
При этом предполагается, что все элементы Wij неотрицательны.
Путь ищется из вершины номер u1 к вершине номер u2 .
Для представления веса, равного бесконечности (машинная бесконечность), используется число GM,
передаваемое в алгоритм.
Это число можно задавать в зависимости от конкретной задачи...
модуль

UNIT Dijkstra;
Interface
Const
 NN=30;
Type
 graph=array [1..nn,1..nn] of integer;

procedure Deikstr(n:integer; W:graph; u1,u2:integer;
                  var length:integer; var Weight:real; var Path: array of integer);
Implementation
procedure Deikstr(n:integer; W:graph; u1,u2:integer;
                  var length:integer; var Weight:real; var Path: array of integer);
var
 i,k,j:integer;
 GM:real;
 d,m:array[1..nn] of real;
 p:array[1..nn] of integer;
 t:integer;
 dd,min:real;
begin
  GM:=10000;{бесконечность}
  length:=0;
  if u1<>u2 then  
  begin
    i:=1;
    repeat
      d[i]:=GM; p[i]:=0; m[i]:=0; i:=i+1
    until not(i<=n);
    d[u1]:=0; t:=u1;
    while length=0 do
    begin
      i:=1;
      repeat
        if w[t,i]<GM then
        begin
          dd:=d[t]+w[t,i];
          if d[i]>dd then begin d[i]:=dd; p[i]:=t  end;
        end;
        i:=i+1
      until not(i<=n);
      Min:=GM; i:=1; k:=0;
      repeat
        if m[i]=0 then
        begin
          if d[i]<min then begin min:=d[i]; k:=i  end;
        end;
        i:=i+1
      until not(i<=n);
      if k<>0  then  begin
        m[k]:=1; t:=k;
        if t=u2 then begin length:=1; end;
      end else begin  length:=-1 end;
    end;
    if length=1 then
    begin
      Path[1]:=u2;  length:=2; j:=u2;
      repeat
        Path[length]:=P[j]; j:=P[j]; length:=length+1
      until not(j<>u1);
      i:=1;  k:=trunc(length/2);
      repeat
        t:=Path[i]; Path[i]:=Path[length-i]; Path[length-i]:=t; i:=i+1
      until not(i<=k);
      length:=length-1
    end;
    Weight:=d[u2]
  end;
end;
end.

демонстрационная программа
компилятор BP7 (target windows)

uses wincrt,dijkstra;
var
 i,u1,u2,n,l:integer;
 G:Graph;
 w:real;
 path:array[0..100] of integer;

procedure ReadFileGraph(var a:graph);
var
 i,j:integer; filename:string; f:text;
begin
 Write('Enter file name:'); readln(filename);
 Assign (f,filename); reset(f);
 Readln(f,N);
 For i:=1 to n do for j:=1 to n do  read(f,a[i,j]); close(f);
end;

begin
 readfilegraph(G); {читаем из файла граф.}
 write('u1 = '); readln(u1); {вводим первую вершину}
 write('u2 = '); readln(u2); {...и конечную..}
 Deikstr(n,G,u1,u2, L,w,path);
 writeln('w=',w:1:2);     {выводим минимальный путь (вес)}
 writeln('path');         {выводим путь ....}
 for i:=1 to l do write(path[i],' - ');
 readkey;
end.

В программе,граф считывается из файла. Вот для такого графа: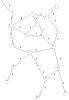

файл должен иметь вид (за машинную бесконечность берется 10000):

20
0 3 10000 10000 10000 10000 10000 10000 10000 10000 10000 10000 10000 10000 10000 10000 10000 10000 10000 10000
3 0 10000 10000 10000 3 10000 10000 10000 10000 10000 10000 10000 10000 10000 10000 10000 10000 10000 10000
10000 10000 0 2 10000 5 1 10000 10000 10000 10000 10000 10000 10000 10000 10000 10000 10000 10000 10000
10000 10000 2 0 3 10000 10000 5 10000 10000 10000 10000 10000 10000 10000 10000 10000 10000 10000 10000
10000 10000 10000 3 0 10000 10000 10000 10000 10000 10000 10000 10000 10000 10000 10000 10000 10000 10000 10000
10000 3 5 10000 10000 0 10000 10000 3 10000 10000 4 10000 10000 10000 10000 10000 10000 10000 10000
10000 10000 1 10000 10000 10000 0 10000 2 2 10000 10000 10000 10000 10000 10000 10000 10000 10000 10000
10000 10000 10000 5 10000 10000 10000 0 10000 10000 4 10000 10000 10000 10000 10000 10000 10000 10000 10000
10000 10000 10000 10000 10000 3 2 10000 0 2 10000 10000 10000 10000 10000 10000 10000 10000 10000 10000
10000 10000 10000 10000 10000 10000 2 10000 2 0 3 10000 10000 10000 10000 10000 10000 10000 10000 10000
10000 10000 10000 10000 10000 10000 10000 4 10000 3 0 10000 4 10000 10000 5 10000 10000 10000 10000
10000 10000 10000 10000 10000 4 10000 10000 10000 10000 10000 0 4 10000 10000 10000 10000 10000 10000 10000
10000 10000 10000 10000 10000 10000 10000 10000 10000 10000 4 4 0 4 3 10000 10000 10000 10000 10000
10000 10000 10000 10000 10000 10000 10000 10000 10000 10000 10000 10000 4 0 10000 10000 3 10000 10000 10000
10000 10000 10000 10000 10000 10000 10000 10000 10000 10000 10000 10000 3 10000 0 10000 10000 3 10000 10000
10000 10000 10000 10000 10000 10000 10000 10000 10000 10000 5 10000 10000 10000 10000 0 10000 4 7 10000
10000 10000 10000 10000 10000 10000 10000 10000 10000 10000 10000 10000 10000 3 10000 10000 0 10000 10000 10000
10000 10000 10000 10000 10000 10000 10000 10000 10000 10000 10000 10000 10000 10000 3 4 10000 0 10000 6
10000 10000 10000 10000 10000 10000 10000 10000 10000 10000 10000 10000 10000 10000 10000 7 10000 10000 0 10000
10000 10000 10000 10000 10000 10000 10000 10000 10000 10000 10000 10000 10000 10000 10000 10000 10000 6 10000 0