| Unconnected |
 29.09.2010 14:25 29.09.2010 14:25
Сообщение
#1
|
 mea culpa      Группа: Пользователи Сообщений: 1 372 Пол: Мужской Реальное имя: Николай Репутация:  24 24  |
Привет всем.)
Столкнулся недавно с интересной задачей (из ЕГЭ какого-то года вроде), звучит примерно так: Человек ходит (бегает) по окружности радиусом 10 м со скоростью 30 м/c (супермен какой то))). Вопрос: под каким углом к поверхности он должен быть, чтобы сохранять равновесие? Во-первых, какой тут характер движения, центробежный разве? По идее, на человека действует центростремительная сила, которая, собсно, и будет выталкивать человека за круг. И скомпенсировать это надо путем перемещения центра массы, чтобы F=mg компенсировала выталкивание. И наклоняться, конечно, надо к центру.. Вот до этого я додумался) Выталкивающая сила будет Fцентр=(mv^2)/r. Только вот mg-то направлена перпендикулярно, под углом 90о, и вроде как совсем не влияет в данном случае на первую силу! И даже если спроецировать mg на oY, не понимаю, как это можно связать с первой силой.. ps: задача 3го уровня ЕГЭ (из 4х). -------------------- "Знаешь, стыдно - когда не видно, что услышал всё, что слушал.."
|
  |
Ответов
| Lapp |
 4.10.2010 9:56 4.10.2010 9:56
Сообщение
#2
|
 Уникум        Группа: Модераторы Сообщений: 6 823 Пол: Мужской Реальное имя: Лопáрь (Андрей) Репутация:  159 159  |
Н-да... чуть прервешься - тут тебе такого наворочают! не разгребешь..
Слушайте, ответить на все я просто физически не в состоянии. Я просто напишу правильный ход рассуждений, сделав акценты на те места, которые вызвали проблемы. Итак, в нашей задаче мы не имеем дело со статическим равновесием. Но это пока - пока мы остаемся в системе отсчета, связанной с поверхностью, по которой бегает атлет. Но если перейти в систему отсчета (СО), вращающуюся вокруг центра круга, по которому бегает атлет - причем, со скоростью атлета - то картина кардинально изменится. В этой СО атлет стоит на месте, и применимо положение о скомпенсированности всех сил, действующих на него. Замечание: все переходы в другие СО, делаюшиеся при решении задач, должны делаться явно. Вращающаяся СО не является инерциальной, а является неинерциальной (НСО). Это означает, что законы Ньютона в ней применимы только при условии, что в них будут учтены т.н. "силы инерции". По определению, сила инерции, действующая на материальную точку массы m, находящуюся в некоторой точке НСО, равна Fi = -ma, где вектор a есть ускорение данной точки НСО. Сила инерции - это очень просто. Это та сила, которая вдавливает вас в спинку сидения разгоняювщегося авто, прижимает в соседке на крутом повороте автобуса, и т.п. Эта сила не подходит под то определение силы, которое привел Un выше. Иначе говоря, СИ не есть сила. Как силы, ее не существует. И правда - ничто не действует на вас, когда машина ускоряется - кроме той самой спинки сидения, которая вдавливается в вас. И никто не прижимает к соседке - наоборот, это ОНА к вам прижимается, поскольку ее толкает на вас стенка автобуса (только не советую ей это объяснять)). Это словосочетание - сила инерции - следует понимать целиком, как некое новообазование - но обходиться с ними можно точно так же, как и с обычними силами. Во вращающейся СО в соответсвии с вышесказанным нужно добавлять силу, равную mV2/R, причем вектор ее следует направлять от центра (в направлении, противоположном центростремительному ускорению). Таким образом, эта сила совершенно законно заслуживает называться центробежной. Важно понимать и помнить, что понятия "центробежная сила" и "центростремительное ускорение" существуют в разных СО и поэтому между собой не пересекаются. В данном случае, например, в СО поверхности атлет бежит (с ускорением, центростремительным) и центробежной силы нету, а во вращающейся СО он стоит (и его ускорение равно нулю), но на него действует (дополнительно к натуральным силам) центробежная сила. Теперь нужно нарисовать картину сил. Вот: 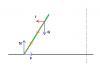 Тут учтены все реальные силы, плюс сила инерции. Поскольку атлет покоится, и ускорение его равно нулю, то все силы должны быть скомпенсированы. Но этого мало, и ответ задачи невозможно получить до тех пор, пока мы не учтем также, что, помимо сил, не должно быть также и нескомпенсированных моментов сил. Это приводит к тому, что оранжевые векторы должны быть не только параллельны и равны по величине, но и лежат на одной прямой, которая пронзает ГГ нашей драмы с макушки до пят.. Таким образом угол наклона атлета равен углу наклона оранжевых векторов. Все. Вопросы? -------------------- я - ветер, я северный холодный ветер
я час расставанья, я год возвращенья домой |
Сообщений в этой теме
 Unconnected Бег по кругу 29.09.2010 14:25
Unconnected Бег по кругу 29.09.2010 14:25
 sheka arctg(g/(v2/r))
[b]Добавлено через 3 мин.
= 6,2... 29.09.2010 14:58
sheka arctg(g/(v2/r))
[b]Добавлено через 3 мин.
= 6,2... 29.09.2010 14:58
 Unconnected
А можно подробнее, почему так? У меня наугад пол... 29.09.2010 15:01
Unconnected
А можно подробнее, почему так? У меня наугад пол... 29.09.2010 15:01
 sheka
[b]Добавлено через 11 мин.
Давай сделаем задач... 29.09.2010 15:35
sheka
[b]Добавлено через 11 мин.
Давай сделаем задач... 29.09.2010 15:35
 Unconnected Хм. На рисунке вид сверху, да? тогда, почему g нап... 29.09.2010 15:58
Unconnected Хм. На рисунке вид сверху, да? тогда, почему g нап... 29.09.2010 15:58
 volvo Чего? Какие 18 градусов? Выдыхай! :) Бежать со... 29.09.2010 16:09
volvo Чего? Какие 18 градусов? Выдыхай! :) Бежать со... 29.09.2010 16:09
 TarasBer При этом мю ботинок об асфальт должен быть около д... 29.09.2010 16:50
TarasBer При этом мю ботинок об асфальт должен быть около д... 29.09.2010 16:50
 Unconnected Жутко извиняюсь, печатал на память, попутал местам... 29.09.2010 16:56
Unconnected Жутко извиняюсь, печатал на память, попутал местам... 29.09.2010 16:56
 volvo Зато угол изменится... Тогда получается как раз 18... 29.09.2010 17:04
volvo Зато угол изменится... Тогда получается как раз 18... 29.09.2010 17:04
 TarasBer > Можете объяснить, какая сила здесь компенсиру... 29.09.2010 17:22
TarasBer > Можете объяснить, какая сила здесь компенсиру... 29.09.2010 17:22
 Unconnected
Во, теперь понял, на примере тамошней задачи про... 29.09.2010 17:56
Unconnected
Во, теперь понял, на примере тамошней задачи про... 29.09.2010 17:56
 sheka
"О чем говорили большевики в 17м году" ... 29.09.2010 18:17
sheka
"О чем говорили большевики в 17м году" ... 29.09.2010 18:17
 Lapp "О чем говорили большевики в 17м году" (... 1.10.2010 6:32
Lapp "О чем говорили большевики в 17м году" (... 1.10.2010 6:32
 Unconnected
Я тоже сначала думал, что это не одно и то же (т... 1.10.2010 6:40
Unconnected
Я тоже сначала думал, что это не одно и то же (т... 1.10.2010 6:40
 sheka
:) Лучшая защита - это нападение:
Решил прочитать... 1.10.2010 18:05
sheka
:) Лучшая защита - это нападение:
Решил прочитать... 1.10.2010 18:05

 Lapp
:) Лучшая защита - это нападение:
Решил прочитать... 1.10.2010 22:27
Lapp
:) Лучшая защита - это нападение:
Решил прочитать... 1.10.2010 22:27

 Lapp Удалось сублимировать осадок? :blum:Осадок? ))
Мак... 2.10.2010 5:01
Lapp Удалось сублимировать осадок? :blum:Осадок? ))
Мак... 2.10.2010 5:01
 Unconnected
Ага)) В процессе экспериментов оказалось, что пр... 2.10.2010 20:54
Unconnected
Ага)) В процессе экспериментов оказалось, что пр... 2.10.2010 20:54
 sheka Вынужден не согласиться. Процитирую:
А кто сказал... 2.10.2010 21:00
sheka Вынужден не согласиться. Процитирую:
А кто сказал... 2.10.2010 21:00
 Unconnected
По кругу она наверное движется круголинейно...или... 2.10.2010 21:04
Unconnected
По кругу она наверное движется круголинейно...или... 2.10.2010 21:04
 sheka :lol: проэкция mg на ОХ(если она горизонтальная) =... 2.10.2010 21:08
sheka :lol: проэкция mg на ОХ(если она горизонтальная) =... 2.10.2010 21:08
 Unconnected
Значит, это была проекция реакции опоры. Численн... 2.10.2010 21:18
Unconnected
Значит, это была проекция реакции опоры. Численн... 2.10.2010 21:18
 TarasBer > Теперь нужно нарисовать картину сил. Вот:
Ка... 4.10.2010 13:23
TarasBer > Теперь нужно нарисовать картину сил. Вот:
Ка... 4.10.2010 13:23
 sheka Ну дык так и есть! 4.10.2010 15:24
sheka Ну дык так и есть! 4.10.2010 15:24
 Lapp Как раз в 10 посте я про это и говорил.Ну дык так ... 4.10.2010 23:17
Lapp Как раз в 10 посте я про это и говорил.Ну дык так ... 4.10.2010 23:17
 sheka Ааа... С детства меня преподы не любили и оценки у... 4.10.2010 23:44
sheka Ааа... С детства меня преподы не любили и оценки у... 4.10.2010 23:44

 Lapp Ааа... С детства меня преподы не любили и оценки у... 5.10.2010 10:57
Lapp Ааа... С детства меня преподы не любили и оценки у... 5.10.2010 10:57
 sheka Буду стараться "усваивать". :) 5.10.2010 16:08
sheka Буду стараться "усваивать". :) 5.10.2010 16:08  |
1 чел. читают эту тему (гостей: 1, скрытых пользователей: 0)
Пользователей: 0

|
Текстовая версия | 4.03.2026 1:52 |








