2 задачи на планиметрию Опции

[Вячеслав Л.]

Прошу помощи:

1. В треугольнике ABC точка N - точка пересечения высот, CH и AB равны. Найти угол C.

2. В треугольнике ABC ON и BM - высоты, O - центр вписанной окружности. OC=MN=12. Найдите радиус окружности, описанной около треугольника BOC.

Выскажите, пожалуйста, Ваши идеи. Заранее спасибо.

[TarasBer]

1.



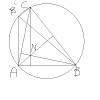Отразим N относительно середины AC, получив B'
т.к ABC+ANC=180, то B' лежит на описанной окружности.
CN=AB'; AB' перпендикулярно AB. Треугольник ABB' - прямоугольный, равнобедренный, значит, AB'B=45, значит, ACB=45

2.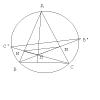



Отразим ортоцентр H относительно сторон AB и AC, получив точки C' и B', лежащие на описанной окружности (это тоже от того, что ABC+AHC=180).
B'C' = 2*MN. MN = R (R - радиус описанной окружности ABC, равен 12) по условию, значит, B'C' - диаметр.
BAC=B'HC, значит сумма дуг C'B и CB' равна дуге BC. Т.к. B'C' диаметр, то C'B+CB'+BC=180, значит, BC=90, значит BOC=90. Значит радиус окружности, описанной вокруг BOC, равен половине BC. Т.к. дуга BC опирается на дугу в 90 градусов, то BC=R*sqrt(2). Значит R(BOC)=R*sqrt(2)/2=6*sqrt(2)