Разложение силы, Тангенциальная и радиальная составляющие Опции

[Tony]

Добрый день.

Вот возник следующий вопрос: допустим у нас имеется твердое тело с центром масс в точке О. К некой точке P этого тела приложена сила F (см. рисунок). Требуется разложить эту силу на радиальную и тангенциальную составляющие, т.е. на силу, 'двигающую' данное тело (Fr), и на силу, 'вращающую' его (Ft).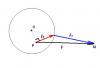



Как я понимаю, вектор радиальной составляющей должен быть направлен из точки О в точку M, a тангенциальной - перпендикулярно OP. При этом в сумме они должны составлять силу F.

Однако попытки применить эти соображения к другим случаям приводят к неудачам: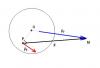



В этом случае Ft и Fr в сумме не равны F.

Собственно, просьба указать на дыру в моих рассуждениях .

[Tony]

Если честно, никакой задачи нет.

Дело в том, что я пишу программу - физический симулятор (ну симулятор - это громко сказано, пока реализованы только столкновения (удары ) тел, трения нет, гравитации тоже ) на основе метода импульсов. Все это дело происходит на плоскости. Тела - произвольные выпуклые многоугольники.

Движение каждого тела характеризуется проекциями линейной скорости Vx и Vy и угловой скоростью W.

Собственно изменение скоростей - линейной и угловой - под действием сил в течение промежутка времени dt происходит следующим образом:

Vx=Vx + dt * Fx / m

Vy=Vy + dt * Fy / m

W=W + dt * T / I

где M - масса тела, I - момент инерции тела.

Если с линейной скоростью все понятно (если F=ma, то массы сократятся, а ускорение * время как раз и дает прирост скорости), то с угловой не очень...Получается, что T - это аналог F для вращательного движения, но получается, что T - скаляр, и как его назвать? Момент силы? Или нет?

Вот собственно и вопрос - если на произвольную точку тела действует внешняя сила, как она отразится на линейной и угловой скоростях...

P.S. Я - школьник, в программе такого нет (по крайней мере у нас), так что если что не так - просьба не пинать .

[Lapp]

я пишу программу - физический симулятор
...
Если с линейной скоростью все понятно (если F=ma, то массы сократятся, а ускорение * время как раз и дает прирост скорости), то с угловой не очень...Получается, что T - это аналог F для вращательного движения, но получается, что T - скаляр, и как его назвать? Момент силы? Или нет?

Вот, теперь дело прояснилось)).
Цель вполне достойная, я поддерживаю и готов помочь, как с физикой так и с программированием.

Да, называют его именно так: момент силы. В общем случае (в трехмерном пространстве) это есть вектор, но, как я понял, ты хочешь имплементить двумерный случай. А в двумерном случае могут осуществляться только два "типа" вращения: по часовой стрлке и против нее. То есть, если все же на секунду выскочить из двумерного пространства, это вращения вокруг оси, перпендикулярной нашему пространству (плоскости). И, соответственно, векторы угловой скорости, ускорения и моментов силы и импульса - все они направленны по одной оси, перпендикулярно этой плоскости. Таким образом, как угловая скорость, так и угловое ускорение, а с ними и момент силы - все они выражаются (каждое) только одним числом, которое является составляющей полного вектора каждой из них, взятой по оси, перпендикулярной плоскости (остальные две составляющих равны нулю). Это еще не дает права называть их скалярами - понятие скаляра несколько более сложно, нежели чем просто представление одним числом. Скорее тут справедливо сравнение со скоростью при рассмотрении движения по прямой (то есть одномерного движения). Там тоже скорость выражается одним числом, но ты же не станешь говорить, что в одномерном движении скорость есть скаляр - так? Если ты не знаком с вращательной механикой, советую тебе ее подучить - хотя, конечно, в двумерном случае можно обойтись этими обрывками - только не называй эти величины скалярами .

При рассмотрении взаимодействия тел к Закону сохранения имнульса (ЗСИ) тебе нужно добавить Закон сохранения момента импульса (ЗСМИ). Это совершенно незавмисимый закон в физике, то есть он не следует из ЗСИ, и тебе без него не обойтись. Если взаимодействие происходит мгновенно (назовем его соударением) и является упругим, то конечное состояние можно вывести без привлечения понятия силы, только на основе применения ЗСИ, ЗСМИ и ЗСЭ. Если же все же нужно рассматривать силы (взаимодействие растянуто во времени), то нужно рассматривать и их моменты относительно выбранной точки. Точка ЦМ во многих случаях удобна, но все же не обязательно использовать именно ее. Если честно, я прямо так с наскока не напишу сейчас все цепочки уравнений, которые тебе нужно запрограммировать, но в принципе это задача решаемая. Думаю, тебе нужно до конца разобраться с ними, прежде чем приступать к программированию. Пиши про свое продвижение и вопросы, я с удовольствием отвечу.
Успехов.