 Компиляция правил для данного раздела
Компиляция правил для данного раздела
1. Заголовок темы должен быть информативным. В противном случае тема закрывается и удаляется ...
2. НЕ используйте форум для личного общения, все что не относится к обсуждению темы - на PM!
3. Одна тема - один вопрос (задача)
4. Спрашивайте и отвечайте четко и по существу!!!
| кучаТрупов |
 15.12.2008 23:01 15.12.2008 23:01
Сообщение
#1
|
|
изувер   Группа: Пользователи Сообщений: 88 Пол: Женский Реальное имя: ann Репутация:  1 1  |
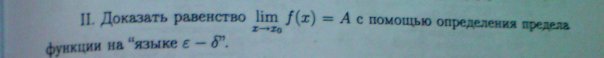 вот само задание.   вот мое абсолютно неправильное решение) пример для предела: lim cos(2-3x)=cos1 при x-->1   а мне нужно решить для примера-- lim ctg(2x+9)=ctg3 при x-->-3 определение предела на языке эбсэлон-дельта: число А называется пределом(пределом справа,пределом слева) функции f в точке x0 принадлежащей множеству X, если для любого эбсэлон больше нуля существует дельта зависящее от эбселон и большее нуля такое,что для любого х удовлетворяющего неравенству (x0-дельта)<х<(х0 + дельта) выполняется неравенство модуль(f(x)-A)<эбсэлон |
  |
Ответов
| Lapp |
 16.12.2008 5:02 16.12.2008 5:02
Сообщение
#2
|
 Уникум        Группа: Модераторы Сообщений: 6 823 Пол: Мужской Реальное имя: Лопáрь (Андрей) Репутация:  159 159  |
Хорошо, давай сначала .
Делаем замену y=-3+x (тогда x-x0 = x-3 = y). Преобразуем разность функций: ctg(2(-3+y)+9) - ctg(3) = ctg(3+2y) - ctg(3) = cos(3+2y) / sin(3+2y) - cos(3) / sin(3) = (cos(3+2y)*sin(3) - cos(3)*sin(3+2y)) / sin(3+2y) / sin(3) = sin(2y) / (sin(3)*cos(2y)+cos(3)*sin(2y)) / sin(3) Теперь выберем произвольное e (эпсилон). Наша задача: найти такое d (дельта), чтобы при любом y, удовлетворяющем условию 0<y<d выполнялось и |sin(2y) / (sin(3)*cos(2y)+cos(3)*sin(2y))| / |sin(3)| < e . С учетом, что sin(3)>0 : |sin(2y) / (sin(3)*cos(2y)+cos(3)*sin(2y))| < e*sin(3) . Поскольку обе стороны неравенства больше нуля, переворачиваем его (единицу делим на стороны со сменой знака неравенства) : |sin(3)*cos(2y)/sin(2y) + cos(3)| > 1 / (e*sin(3)) . Используем свойство модуля |a-b| => |a| - |b| , завышаем требования: |sin(3)*cos(2y)/sin(2y)| - |cos(3)| > 1 / (e*sin(3)) - если выполнено это, то выполнено и то. Так как cos(3)~-0.99<0, то |cos(3)|=-cos(3). Переносим его вправо: |sin(3)*cos(2y)/sin(2y)| > 1/e/sin(3) - cos(3) Так как sin(3)~0.14>0 , то: |cos(2y)/sin(2y)| > (1/e/sin(3) - cos(3)) / sin(3) = M - обозначим M для простоты. Еше раз переворачиваем: |sin(2y)/cos(2y)| < 1/M . Выберем d<Pi/6 , тогда cos(2y)>1/2>0 Получаем: |sin(2y)| < cos(2y)/M . Снова загрубляем, заменяя косинус на 1/2: |sin(2y)| < 1/2/M. Используя |sin(x)|<=|x| , снова загрубляем неравенство: |2y| < 1/2/M , или: |y| < 1/4/M - снова, если выолнено это, то выполнено и то. Это значит, что можно взять d=1/4/M , то есть: d = sin(3) / (1/e/sin(3) - cos(3)) / 4 . Осталось пересечь с наложенным ранее условием d<Pi/6, и это и есть искомая дельта. Надеюсь, не ошибся в арифметике . Отвык я от нее.. Добавлено через 10 мин. Стремление синуса к нулю эквивалентно в определенном смысле неравенству |sin(x)|<|x|, которое использовано в методичке. Так что я свел к нему. -------------------- я - ветер, я северный холодный ветер
я час расставанья, я год возвращенья домой |
Сообщений в этой теме
 кучаТрупов доказать на языке эпсилон-дельта 15.12.2008 23:01
кучаТрупов доказать на языке эпсилон-дельта 15.12.2008 23:01
 Lapp определение предела на языке эбсэлон-дельта:
число... 15.12.2008 23:25
Lapp определение предела на языке эбсэлон-дельта:
число... 15.12.2008 23:25
 кучаТрупов ээ Оо с методички переписывала же.
число А называ... 15.12.2008 23:27
кучаТрупов ээ Оо с методички переписывала же.
число А называ... 15.12.2008 23:27

 Lapp Молодец :)
Ключевые слова именно вот эти:
не равно... 16.12.2008 0:12
Lapp Молодец :)
Ключевые слова именно вот эти:
не равно... 16.12.2008 0:12
 кучаТрупов икс стремится к минус трем)тоесть все получается)
... 16.12.2008 0:18
кучаТрупов икс стремится к минус трем)тоесть все получается)
... 16.12.2008 0:18

 Lapp икс стремится к минус трем)тоесть все лучается)
Ой... 16.12.2008 0:22
Lapp икс стремится к минус трем)тоесть все лучается)
Ой... 16.12.2008 0:22

 Lapp ctg(2(-3+d)+9) - ctg(3) =
ctg(3+2d) - ctg(3) =
c... 16.12.2008 0:47
Lapp ctg(2(-3+d)+9) - ctg(3) =
ctg(3+2d) - ctg(3) =
c... 16.12.2008 0:47
 кучаТрупов нет. это не доказано..но ведь доказательство по за... 16.12.2008 0:56
кучаТрупов нет. это не доказано..но ведь доказательство по за... 16.12.2008 0:56

 Lapp нет. это не доказано..но ведь доказательство по за... 16.12.2008 1:34
Lapp нет. это не доказано..но ведь доказательство по за... 16.12.2008 1:34
 кучаТрупов
|a-b| => |a| - |b|
все решение оч клевое)
... 16.12.2008 13:23
кучаТрупов
|a-b| => |a| - |b|
все решение оч клевое)
... 16.12.2008 13:23

 Lapp но вот эта штука..по свойству как нам говорили- мо... 16.12.2008 13:47
Lapp но вот эта штука..по свойству как нам говорили- мо... 16.12.2008 13:47
 кучаТрупов |sin(2y)| < 1/2/M.
Используя |sin(x)|<=|x| ... 20.12.2008 1:33
кучаТрупов |sin(2y)| < 1/2/M.
Используя |sin(x)|<=|x| ... 20.12.2008 1:33

 Lapp --исходя из того что синус в исходном(верхнем)нера... 20.12.2008 3:16
Lapp --исходя из того что синус в исходном(верхнем)нера... 20.12.2008 3:16
 кучаТрупов ну здорово^_^спасибо)теперь я спокойна)) :rolleyes... 20.12.2008 13:02
кучаТрупов ну здорово^_^спасибо)теперь я спокойна)) :rolleyes... 20.12.2008 13:02
 кучаТрупов непринятое решение
принятое решение
27.12.2008 17:53
кучаТрупов непринятое решение
принятое решение
27.12.2008 17:53

 Lapp непринятое решениеВ непринятом решении у тебя груб... 28.12.2008 7:31
Lapp непринятое решениеВ непринятом решении у тебя груб... 28.12.2008 7:31
 кучаТрупов нет. к этому слову не придралась она. ей в неприня... 28.12.2008 15:16
кучаТрупов нет. к этому слову не придралась она. ей в неприня... 28.12.2008 15:16

 Lapp но она еще много к чему придиралась)
кучаТрупов, ... 28.12.2008 15:37
Lapp но она еще много к чему придиралась)
кучаТрупов, ... 28.12.2008 15:37
 кучаТрупов я с ней спорила 40 минут. меня возненавидила вся г... 28.12.2008 15:40
кучаТрупов я с ней спорила 40 минут. меня возненавидила вся г... 28.12.2008 15:40
 Lapp я с ней спорила 40 минут. меня возненавидила вся г... 28.12.2008 15:46
Lapp я с ней спорила 40 минут. меня возненавидила вся г... 28.12.2008 15:46  |
1 чел. читают эту тему (гостей: 1, скрытых пользователей: 0)
Пользователей: 0

|
Текстовая версия | 9.12.2025 0:24 |








