 Компиляция правил для данного раздела
Компиляция правил для данного раздела
1. Заголовок темы должен быть информативным. В противном случае тема закрывается и удаляется ...
2. НЕ используйте форум для личного общения, все что не относится к обсуждению темы - на PM!
3. Одна тема - один вопрос (задача)
4. Спрашивайте и отвечайте четко и по существу!!!
| 3 kilos |
 2.05.2006 20:41 2.05.2006 20:41
Сообщение
#1
|
|
Новичок  Группа: Пользователи Сообщений: 28 Пол: Мужской Репутация:  0 0  |
Давным давно натыкался на очень интересную задачу, когда плотнику дана дощечка площадью поверхности S1, дана дырка площадью S2. (s1 не равно s2). И этот хитрый плотник каким-то образом так распилил дащечку на несколько трапеций и треугольников, перестановил их и получил дощечку, которая закрывала дырку, площадью S2. Т.Е. Он каким-то образом из одной площади получил другую.
Я точно помню, что решение данной задачи приводилось в книжке, поэтому задачка вбилась в память. А вот теперь хочется узнать, как он так получил. Может кто натыкался на такую задачку в книжках типа "Задачи на Смекалку"? |
  |
Ответов(1 - 12)
| APAL |
 2.05.2006 21:51 2.05.2006 21:51
Сообщение
#2
|
 Смотрю...      Группа: Модераторы Сообщений: 1 055 Пол: Мужской Реальное имя: Пшеничный Алексей Анатольевич Репутация:  6 6  |
Думаю условие не полностью приведено. Нельзя простым распиливанием увеличить площадь.
-------------------- |
| 3 kilos |
 2.05.2006 22:23 2.05.2006 22:23
Сообщение
#3
|
|
Новичок  Группа: Пользователи Сообщений: 28 Пол: Мужской Репутация:  0 0  |
Думаю условие не полностью приведено. Нельзя простым распиливанием увеличить площадь. Я точно не помню, увеличивается площадь или уменьшается, НО она изменяется. Я сам тогда был слегка шокирован, поэтому задачка мне запомнилась. Ладно, придется мне идти в библиотеки и перелистывать все книги с задачами на смекалку. |
| GoodWind |
 3.05.2006 6:53 3.05.2006 6:53
Сообщение
#4
|
 Автооответчик      Группа: Модераторы Сообщений: 1 188 Пол: Мужской Реальное имя: Александр Репутация:  16 16  |
тут была похожая задача с треугольником...
-------------------- Неадекватная чушь может быть адекватным ответом на неадекватный вопрос. Понятно или разжевать?
|
| Lapp |
 3.05.2006 7:31 3.05.2006 7:31
Сообщение
#5
|
 Уникум        Группа: Модераторы Сообщений: 6 823 Пол: Мужской Реальное имя: Лопáрь (Андрей) Репутация:  159 159  |
тут была похожая задача с треугольником...  Тут именно как бы изменяется площадь! Может, та головоломка похожа на эту? Только в этой очень существенно, что это треугольник (хотя бы одна сторона должна быть наклонной). Хотел сказать ответ - да раздумал.. Вдруг кто-то не знает? -------------------- я - ветер, я северный холодный ветер
я час расставанья, я год возвращенья домой |
| -Дож- |
 3.05.2006 15:55 3.05.2006 15:55
Сообщение
#6
|
|
Гость |
Объемную фигуру разрезать на части и сложить из них новую фигуру, объемом больше данной
можно. Но с плоской фигурой это невозможно. |
| 3 kilos |
 3.05.2006 16:04 3.05.2006 16:04
Сообщение
#7
|
|
Новичок  Группа: Пользователи Сообщений: 28 Пол: Мужской Репутация:  0 0  |
Ну из двух треугольников можно сделать прямоугольник, значит площадь уменьшается.. !??!??!?!?
Значит площадь плоской фигуры можно изменить(неважно что там стороны наклонены) ???? Цитата(lapp) Только в этой очень существенно, что это треугольник (хотя бы одна сторона должна быть наклонной). 1 - А как у треугольника хотябы одна сторона не сможет быть наклонной? 2 - Есть еще какиенить примеры парадокса площадей? 3 - Скажи пож-то ответ, меняется тут площадь или нет? Раз треуголльник занимал какуюто площадь сначала, а после перестаноновки этуже площадь занимает не всю, значит площадь новой фигуры изменилась???!?!?!?!? Но сумма площадей маленьких фигурок же всегда остается неизменной.. Я щас слегка шокирован правда Может кто-нить обьяснить в чем дело? Я уже сегодня к лектору по физике подходил. Сообщение отредактировано: 3 kilos - 3.05.2006 16:31 |
| volvo |
 3.05.2006 16:35 3.05.2006 16:35
Сообщение
#8
|
|
Гость |
3 kilos, ты ВНИМАТЕЛЬНО читай, что тебе пишут, ОК?
Цитата Только в этой очень существенно, что это треугольник (хотя бы одна сторона должна быть наклонной). Красным выделена ПРИЧИНА, по которой это существенно; не путай причину и следствие... |
| 3 kilos |
 3.05.2006 16:38 3.05.2006 16:38
Сообщение
#9
|
|
Новичок  Группа: Пользователи Сообщений: 28 Пол: Мужской Репутация:  0 0  |
volvo
Извеняюсь, я сказал чушь. Просто я слегка замешан. Будь добр, ответь тогда мне на третий вопрос, я вижу ты внимательно читаешь. Сообщение отредактировано: 3 kilos - 3.05.2006 16:39 |
| APAL |
 3.05.2006 16:43 3.05.2006 16:43
Сообщение
#10
|
 Смотрю...      Группа: Модераторы Сообщений: 1 055 Пол: Мужской Реальное имя: Пшеничный Алексей Анатольевич Репутация:  6 6  |
Не меняется площадь.
-------------------- |
| 3 kilos |
 3.05.2006 16:48 3.05.2006 16:48
Сообщение
#11
|
|
Новичок  Группа: Пользователи Сообщений: 28 Пол: Мужской Репутация:  0 0  |
Я кажется понял в чем хитрость. Красный и зеленый треугольники подобны( сначало кажется, т.к. ихние гипотенузы принадлежат одной большой гипотенузе), значит должны быть подобны их стороны. Но эта подобность не наблюдается, 8/5 не равно 3/2. Площадь никуда не девается.
Следовательно пустота на втором рисунке компенсирует выпуклость, создаваемая гипотенузами треугольников. Когдаже в первом случае, пустоты нету, зато гипотенузами треуг-ов создается вогнутость. Сообщение отредактировано: 3 kilos - 3.05.2006 17:00 |
| APAL |
 3.05.2006 16:59 3.05.2006 16:59
Сообщение
#12
|
 Смотрю...      Группа: Модераторы Сообщений: 1 055 Пол: Мужской Реальное имя: Пшеничный Алексей Анатольевич Репутация:  6 6  |
Достаточно проверить условия равенства углов в красном и темно-зеленом треугольнике.
Для красного угол = arccos(3*SQRT(8^2+3^2)) = arccos(3*8.544) = arccos(25.632) Для темно-зеленого = arccos(2*SQRT(5^2+2^2)) = arccos(2*5.385) = arccos(10.77) Надеюсь я не ошибся в расчетах... давно не занимался тригонометрией. -------------------- |
| Lapp |
 4.05.2006 0:31 4.05.2006 0:31
Сообщение
#13
|
 Уникум        Группа: Модераторы Сообщений: 6 823 Пол: Мужской Реальное имя: Лопáрь (Андрей) Репутация:  159 159  |
пустота на втором рисунке компенсирует выпуклость, создаваемая гипотенузами треугольников. Когдаже в первом случае, пустоты нету, зато гипотенузами треуг-ов создается вогнутость. Именно так. Эти две фигури (на рисунке) очень похожи на треугольники, но на самом деле они обе являются четурехугольниками. "Гипотенуза" на самом деле в обоих случаях представляет собой ломаную. Для того, чтобы излом был меньше заметен, эта линия должна быть наклонена (трудно спрятать излом горизонтальной или вертикальной линии, я считаю, особенно на клетчатой бумаге). Я привел эту задачку к тому, что в искомой задаче про плотника могло быть нечто подобное. Объемную фигуру разрезать на части и сложить из них новую фигуру, объемом больше данной можно. Но с плоской фигурой это невозможно. Дож, речь в твоей ссылке идет не об объеме (там, кстати, это оговаривается). Подобные фокусы действительно поражают, но не имеют большого отношения к делу. И кстати, размерность тут ни при чем абсолютно. Вот, посмотри на эту картинку: 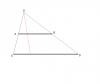 Легко видеть, что каждой точке верхнего отрезка ставится в соответствие ровно одна точка нижнего. При этом нижний в два раза длиннее. Кажется, что этот рисунок доказывает, что они равны по длине. Этому удивлялись еще древние греки, пока не было введено корректное понятие меры. -------------------- я - ветер, я северный холодный ветер
я час расставанья, я год возвращенья домой |
  |
1 чел. читают эту тему (гостей: 1, скрытых пользователей: 0)
Пользователей: 0

|
Текстовая версия | 26.07.2025 21:01 |









