 Прочтите прежде чем задавать вопрос!
Прочтите прежде чем задавать вопрос!
1. Заголовок темы должен быть информативным. В противном случае тема удаляется ...
2. Все тексты программ должны помещаться в теги [code=pas] ... [/code].
3. Прежде чем задавать вопрос, см. "FAQ", если там не нашли ответа, воспользуйтесь ПОИСКОМ, возможно такую задачу уже решали!
4. Не предлагайте свои решения на других языках, кроме Паскаля (исключение - только с согласия модератора).
5. НЕ используйте форум для личного общения, все что не относится к обсуждению темы - на PM!
6. Одна тема - один вопрос (задача)
7. Проверяйте программы перед тем, как разместить их на форуме!!!
8. Спрашивайте и отвечайте четко и по существу!!!
  |
| Vasya! |
 9.10.2006 16:21 9.10.2006 16:21
Сообщение
#1
|
|
Новичок  Группа: Пользователи Сообщений: 35 Пол: Мужской Реальное имя: Вася Репутация:  0 0  |
Говорят, что копьютер вычислял-вычислял и вычислил (например за трое суток) 500 000 000 знаков.
А как вычисляется число Пи? |
| klem4 |
 9.10.2006 16:23 9.10.2006 16:23
Сообщение
#2
|
 Perl. Just code it!       Группа: Модераторы Сообщений: 4 100 Пол: Мужской Реальное имя: Андрей Репутация:  44 44  |
-------------------- perl -e 'print for (map{chr(hex)}("4861707079204E6577205965617221"=~/(.{2})/g)), "\n";'
|
| Vasya! |
 9.10.2006 16:31 9.10.2006 16:31
Сообщение
#3
|
|
Новичок  Группа: Пользователи Сообщений: 35 Пол: Мужской Реальное имя: Вася Репутация:  0 0  |
Это я видел. А я бы хотел понять алгоритм нахождения числа (и желательно больше 54 000).
|
| volvo |
 9.10.2006 16:49 9.10.2006 16:49
Сообщение
#4
|
|
Гость |
Цитата и желательно больше 54 000 Переходи на 32 бита, где длина строки может достигать 2 Gb, и вычисляй сколько нужно знаков... В ДОС-овском Паскале ты ограничен размером сегмента, отсюда и ограничение на число символов... |
| Vasya! |
 9.10.2006 17:38 9.10.2006 17:38
Сообщение
#5
|
|
Новичок  Группа: Пользователи Сообщений: 35 Пол: Мужской Реальное имя: Вася Репутация:  0 0  |
А как насчет принципа, алгоритма вычисления числа.
|
| volvo |
 9.10.2006 18:22 9.10.2006 18:22
Сообщение
#6
|
|
Гость |
Я же написал в теме по ссылке, что не имею понятия об алгоритме. Невнимательно читал?
Погугли на тему "BBP - Formula", "Bailey-Borwein-Plouffe Formula"... Что-нибудь да найдется |
| Vasya! |
 9.10.2006 18:28 9.10.2006 18:28
Сообщение
#7
|
|
Новичок  Группа: Пользователи Сообщений: 35 Пол: Мужской Реальное имя: Вася Репутация:  0 0  |
Спасибо and sorry!!!
|
| Lapp |
 10.10.2006 1:59 10.10.2006 1:59
Сообщение
#8
|
 Уникум        Группа: Модераторы Сообщений: 6 823 Пол: Мужской Реальное имя: Лопáрь (Андрей) Репутация:  159 159  |
Алгоритмов существет много разных. Самый простой и понятный - формула Лейбница:
П/4 = 1 - 1/3 + 1/5 - 1/7 + 1/9 - 1/11 + .. Поскольку ряд знакопеременный с убывающим по модулю общим членом, то точность конечной суммы оценивается последним членом. То есть написанный выше кусок даст примерно точность до первого знака после запятой, а если нужно, например, точность до третьего знака, 0.001 (одна тысячная) , то нужно взять сумму, заканчивающуюся членом 1/1001, то есть примерно 500 членов ряда. Извиняюсь в посте была ошибка. Сейчас исправлено (выделено зеленым цветом) Сообщение отредактировано: lapp - 10.10.2006 5:39 -------------------- я - ветер, я северный холодный ветер
я час расставанья, я год возвращенья домой |
| Lapp |
 10.10.2006 6:03 10.10.2006 6:03
Сообщение
#9
|
 Уникум        Группа: Модераторы Сообщений: 6 823 Пол: Мужской Реальное имя: Лопáрь (Андрей) Репутация:  159 159  |
Понятно, что формула Лейбница сходится очень медленно. Вот этот ряд сходится гораздо скорее:
П/(2*Sqrt(3) = 1 - (1/3)(1/3) + (1/5)(1/3)^2 - (1/7)(1/3)^3 + (1/9)(1/3)^4 - (1/11)(1/3)^5 + ... Приведенный его фрагмент обеспечивает точность лучше одной сотой, а если добавить еще всего один член, то будет 0.001, на достижение которой с формулой Лейбница уходит 500 членов. -------------------- я - ветер, я северный холодный ветер
я час расставанья, я год возвращенья домой |
| Vasya! |
 11.10.2006 18:36 11.10.2006 18:36
Сообщение
#10
|
|
Новичок  Группа: Пользователи Сообщений: 35 Пол: Мужской Реальное имя: Вася Репутация:  0 0  |
А если вычислять по формуле Лейбница, то этот процесс понятно, что долгий, но он точный?
|
| Lapp |
 12.10.2006 3:24 12.10.2006 3:24
Сообщение
#11
|
 Уникум        Группа: Модераторы Сообщений: 6 823 Пол: Мужской Реальное имя: Лопáрь (Андрей) Репутация:  159 159  |
А если вычислять по формуле Лейбница, то этот процесс понятно, что долгий, но он точный? Я же написал оценку точности! Или ты думаешь, что это теория, которая типа сама по себе, а практика сама по себе?... Повторяю: любой знакопеременный ряд с убывающим по модулю общим членом оценивается следующим образом (в предположении, что An<0, а A(n+1)>0 ) : Sn < S < S(n+1) , где S - бесконечеая сумма. Вычитая из правого неравенства Sn, имеем: S - Sn < S(n+1) - Sn = A(n+1) Поскольку обе стороны положительны, можем поставить модули |S - Sn| < |S(n+1) - Sn| = |A(n+1)| Я не буду доказывать эту формулу для An>0, это практически очевидно. Сказанное можно проиллюстрировать картинкой: 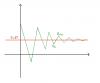 Короче, имеем следующее: Несмотря на то, что мы не знаем бесконечной суммы и не можем ее узнать, мы можем сказать, что всякая n-ная конечная сумма отличается от нее по модулю не более, чем модуль следующего члена ряда. Иначе говоря, если мы знаем, что |An|=0.001, то для того, чтобы получить точность в одну тысячную, нам достаточно сложить n-1 членов ряда. Теперь ясно? -------------------- я - ветер, я северный холодный ветер
я час расставанья, я год возвращенья домой |
| Reflex |
 12.10.2006 6:54 12.10.2006 6:54
Сообщение
#12
|
 Пионер   Группа: Пользователи Сообщений: 118 Пол: Женский Репутация:  0 0  |
есть еще алгоритм через арктангенсы как-то...
-------------------- Нам не дано предугадать как наше слово отзовется...
|
| Lapp |
 12.10.2006 7:07 12.10.2006 7:07
Сообщение
#13
|
 Уникум        Группа: Модераторы Сообщений: 6 823 Пол: Мужской Реальное имя: Лопáрь (Андрей) Репутация:  159 159  |
есть еще алгоритм через арктангенсы как-то... Уважаемая Reflex, да будет тебе известно, что вторая из приведенных мной формул и есть разложение арктангенса в ряд.. -------------------- я - ветер, я северный холодный ветер
я час расставанья, я год возвращенья домой |
| Vasya! |
 16.10.2006 20:45 16.10.2006 20:45
Сообщение
#14
|
|
Новичок  Группа: Пользователи Сообщений: 35 Пол: Мужской Реальное имя: Вася Репутация:  0 0  |
Огромное спасибо!!! Буду пока разбираться с тем что есть.
Кстати С Днем Рождения!!! |
| Vasya! |
 22.10.2006 12:54 22.10.2006 12:54
Сообщение
#15
|
|
Новичок  Группа: Пользователи Сообщений: 35 Пол: Мужской Реальное имя: Вася Репутация:  0 0  |
Иначе говоря, если мы знаем, что |An|=0.001, то для того, чтобы получить точность в одну тысячную, нам достаточно сложить n-1 членов ряда.
Вот это не очень ясно! Пример какой-то можешь привести. |
| Lapp |
 22.10.2006 14:09 22.10.2006 14:09
Сообщение
#16
|
 Уникум        Группа: Модераторы Сообщений: 6 823 Пол: Мужской Реальное имя: Лопáрь (Андрей) Репутация:  159 159  |
Вот это не очень ясно! Пример какой-то можешь привести. Какой пример?.. Я привел тебе точное математическое доказательство! Да еще и с рисунком!! Дай себе труд всмотреться в график - и ты все поймешь, там нет ничего сложного. Или уж открой любой учебник по матану, найди там тему знакопеременные ряды, прочти доказательство еще раз. А пример - ты, в конце концов его сам и делаешь. Так трудно закодировать несколько строк и убедиться? Код { Calculation the Pi, Liebniz formula } var i,n:integer; s,z:real; begin Write(' N = ');ReadLn(n); s:=0; z:=1; for i:=1 to n-1 do begin s:=s+z*1/(2*i-1); z:=-z end; WriteLn(' An = ',(1/n):10:8); WriteLn(' S(n-1) = ',s:10:8); WriteLn(' Pi/4 = ',(Pi/4):10:8); WriteLn(' 4*S(n-1) = ',(4*s):10:8); WriteLn(' Pi = ',Pi:10:8); ReadLn end. -------------------- я - ветер, я северный холодный ветер
я час расставанья, я год возвращенья домой |
  |
1 чел. читают эту тему (гостей: 1, скрытых пользователей: 0)
Пользователей: 0

|
Текстовая версия | 15.11.2025 13:16 |









